
线性代数笔记
基于期末卷子
章节整理
一、线性方程组解的结构

1.高斯消元法
高斯消元(阶梯形式EF)
使用表示成AX=b的矩阵
其中A表示的是对应的系数矩阵,b是解的线性组合
将系数矩阵和右端向量合在一起构成的矩阵B=(A b)称为增广矩阵
通过一系列的行初等变换把这个增广矩阵转换为“简化阶梯矩阵”,就可以得出对应的解了。
2.线性方程组的可解性
线性方程组有解的充要条件是系数矩阵的秩等于增广矩阵的秩,且当两个矩阵的秩均为n有唯一解,<n则有无穷多解
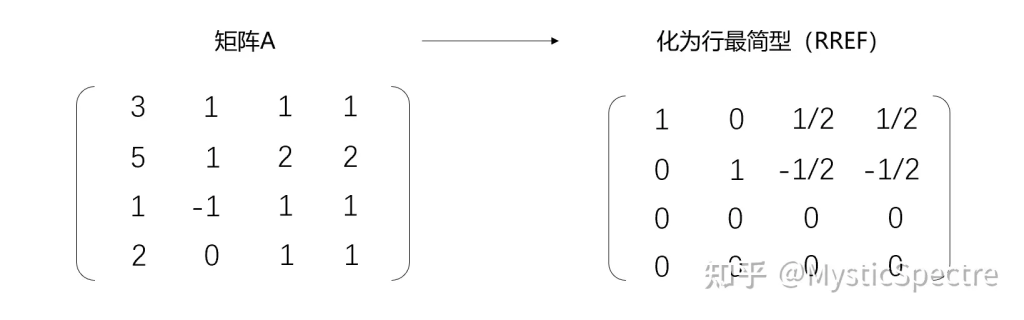
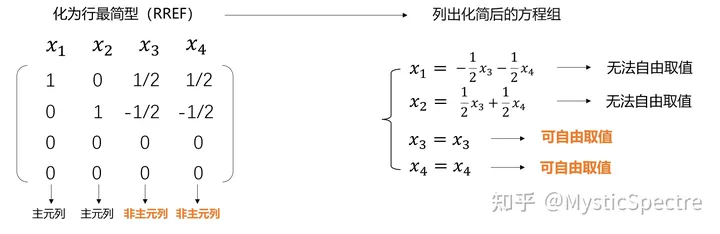
然后根据列出的关系式,实现最后的基础解系
非齐次线性方程组解的结构:特解+齐次方程通解
线性无关
by examples

线性相关的核心要求,就是一组向量,其中任意一个向量都能通过其他向量的线性组合表示,或者采用方程的视角
线性无关的定义如下:
一组向量 {v₁, v₂, …, vₙ} 在线性空间中是线性无关的,如果不存在非零标量 {c₁, c₂, …, cₙ} 使得以下方程成立:
c₁v₁ + c₂v₂ + … + cₙvₙ = 0
其中,0 是零向量。如果上述方程的唯一解是所有系数 c₁, c₂, …, cₙ 都等于零,则这组向量是线性无关的。这可以写成数学表达式的形式如下:
如果方程 c₁v₁ + c₂v₂ + … + cₙvₙ = 0 有唯一解 c₁ = c₂ = … = cₙ = 0,则向量集合 {v₁, v₂, …, vₙ} 是线性无关的。
矩阵的秩
与基础解系的关系


与基础解系相关的内容总结:
基础解系是指方程组的解集的极大线性无关组,即若干个无关的解构成的能够表示任意解的组合。基础解系需要满足三个条件:(1)基础解系中所有量均是方程组的解;(2)基础解系线性无关,即基础解系中任何一个量都不能被其余量表示;(3)方程组的任意解均可由基础解系线性表出,即方程组的所有解都可以用基础解系的量来表示。
“秩r=极大线性无关组中向量的个数,”
AX=0,作用对象是A,求的是A的秩,求的是线性方程组里“有效”的方程的个数。(线性相关的视为重复无效)
“基础解系本身又是一个极大线性无关组,”
一组基础解系,是指AX=0求X时,能用最“简洁”的一组解表达出所有的解(就是所谓的通解),作用对象是X。为了最“简洁”,它们就得线性无关;为了能表达出“所有”,它们就得“极大”涵盖所有情况。
“但其所含向量个数为n-r,”
这种求AX=0的X的通解的情况(A不满秩时多解),是用自由变量表示出所有的变量。n-r正是自由变量的个数。这里的向量个数与A的秩挂钩,等于A满秩情况的秩-A实际情况的秩。
“那极大线无关组所含向量个数到底是r还是n-r?”
其实就是,极大线性无关描述的是方程个数还是解向量(的基础解系)个数,如果是方程是r(A)=r,如果是解向量(的基础解系)是n-r。
作者:不知名小动物
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

注:一个矩阵假如行列式为零则不满秩





关于一些秩的性质的具体证明


特征值与特征向量(以及相似矩阵)


行列式的计算及技巧
以题代学
https://zhuanlan.zhihu.com/p/346885185


或者采取数学归纳和分拆并举的方式执行

重要定理:

把第i行的元素加到第j行元素上(行列式值不变),再将行列式按第j行展开,得
D = (aj1 + ai1)Aj1 + (aj2 + ai2)Aj2 + …… + (ajn + ain)Ajn
= D + (ai1Aj1 + ai2Aj2 + …… + ainAjn)
所以上式后面部分为0
克莱默法则




