Linear Algebra basics
Contents
课程基本要求
about homework: 教学立方纸质转电子
link: https://teaching.applysquare.com/S/Course/index/cid/30898
线性代数基本介绍
线性代数,简单来讲,就是一种有关“多维变量”,或者转换为“向量”,的一系列数学,主要是线性方程组的问题,以及多维变量之间的运算变换问题
所谓“线性”,即所有有关的研究对象以及计算都是基于“一次线性”发生的
向量,在线性代数里面特化为只有一行或者一列的矩阵,维度由“长度”或者“宽度”决定
线性代数的部分直接应用
求解线性方程组/线性变换表示/二次曲线分类(二次型相关)(通过整理矩阵对角线系数来针对二次曲线分类)/推广了数的表示范围(斐波那契推导)
第一章:行列式基础
行列式的定义:
将n个可以进行乘法或者加法运算的元素排列成n行n列,在本文范围内一般表示一个值或者是一个带未知数的式子。
一阶行列式的值定义为
$$
D_1 = det(a_{11}) = a_{11}
$$
余子式和逆序数的定义
余子式:在 n阶行列式 中,划去元aij所在的第i行与第j列的元,剩下的元不改变原来的顺序所构成的n-1阶行列式
代数余子式:设|𝐴|是一个 𝑛 阶行列式,𝑀𝑖𝑗是|𝐴|的第(𝑖,𝑗)元素的余子式,定义|𝐴|的第(𝑖,𝑗)元素的代数余子式为:
$$
A_y = (-1)^{i+j}M_{ij}
$$
行列式默认行列数目一致(可计算的基础),二三阶的行列式可以用“对角线法则”,但是维度上升之后就 不能通用了
因此需要给出高阶行列式的计算方法
按照某一行or某一列展开进行分割计算。
因此可以给出行列式的逆序数定义:
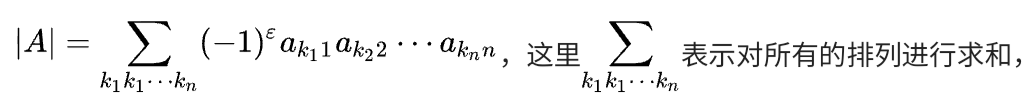
下附加余子式定义
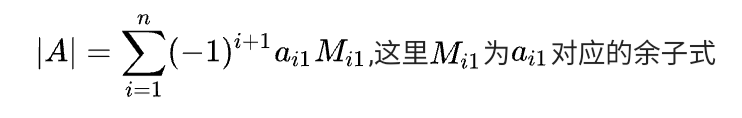
行列式的性质
1.行列式与他的转置行列式值相等
2.交换行列式其中的两行(列),则行列式的值变成其相反数(差一个负号)
3.任意两行(列)相等的行列式值为0
4.行列式可以按任一行(列)展开
5.如果两行(列)对应成比例,则行列式的值为0
6.行列式的第i行的每一个元素都可以表示为两数的和,则该行列式可以表示为两个行列式之和
7.将行列式的任意一行(列)加到另一行(列)上去 ,行列式不变
8.行列式任一行(列)的元素与另一行(列)元素的代数余子式对应乘积之和为零
n阶范德蒙德行列式

crammer法则


行列式计算
线性代数几种特殊类型行列式_及其计算_爪型行列式-CSDN博客

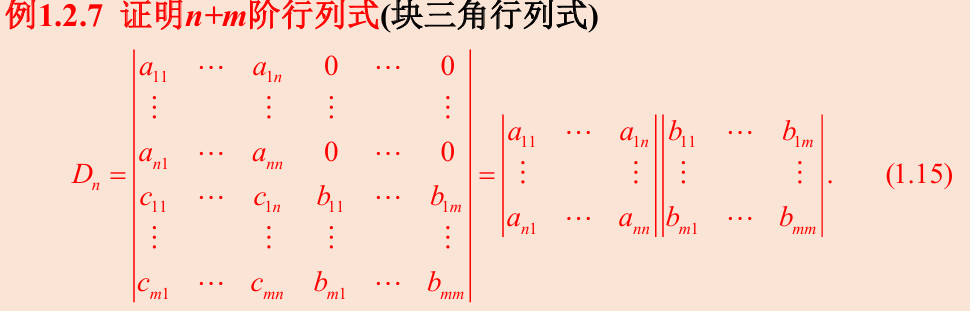
矩阵和向量
definition:
由m*n个数排成m行n列表称为矩阵,n个数字组成的有序数组可以成为n维向量,有行列之分
对角矩阵:记作diag()


方阵的行列式:
如果|A|为0,则A为奇异矩阵
方阵A=(aij)n×n的行列式,记为|A| . 如果|A|≠0,则称矩阵A
是非异矩阵,如果|A|=0,则称矩阵A是奇异矩阵或退化矩阵.
矩阵乘法:
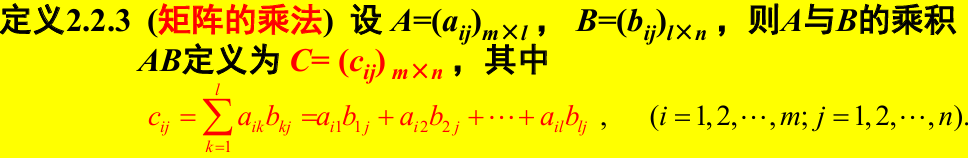
矩阵的加法运算
加法基本性质:交换/结合/零矩阵
矩阵的数乘运算
满足基本的结合律和分配律
矩阵的乘法
矩阵乘法无交换律
转置矩阵:行列互换之后得到的矩阵
Basic properties of transpose matrices: |A| = |AT| (A+B)转置 (AB)t = BT*AT
乘法最基本性质:
- 结合律:(AB)C=A(BC) .
- 数乘结合律:k(AB) =(kA)B= A (kB) .
- 分配律:A(B+C)=AB+AC;(B+C)A=BA+CA
转置矩阵:
转置基本性质:
- (AT)T=A ; |AT|=|A| ;
- (A+B)T=AT+BT ;
- (kA)T=kAT (k,l均是数);
- (AB)T=BTAT .

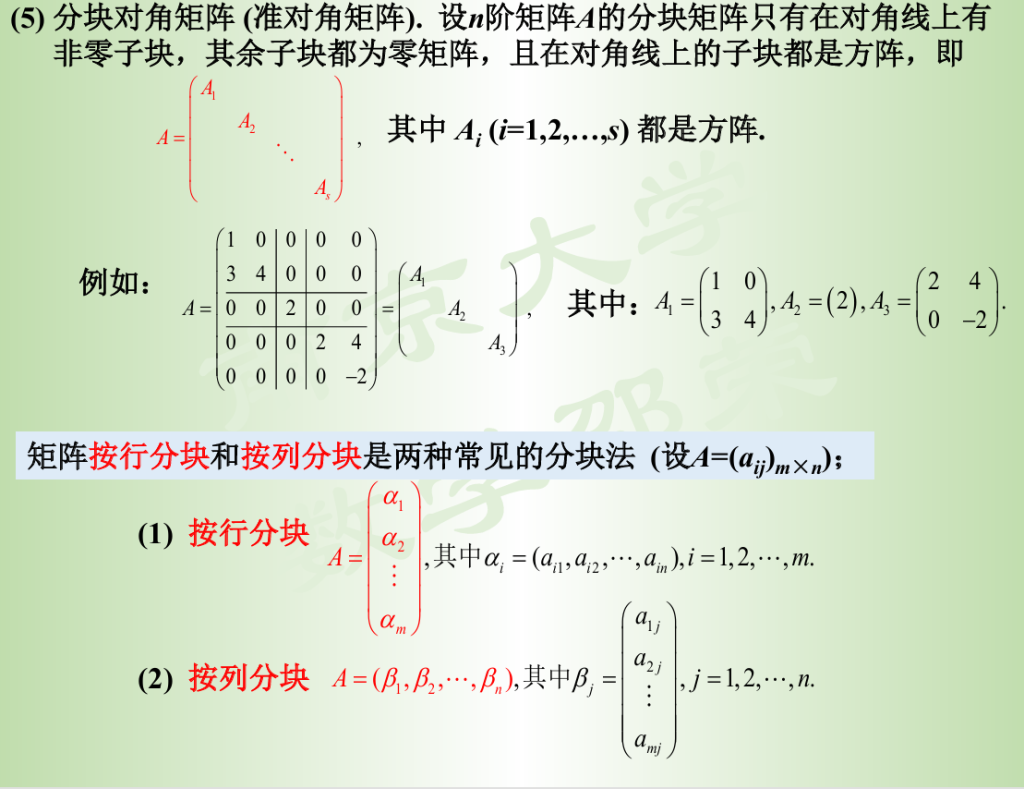
分块矩阵





逆矩阵
逆矩阵的基本性质
- 若A可逆,则A-1也是可逆的,并且他们的行列式互为倒数
- 若A可逆,则kA可逆
- 若A可逆,则A转置也可逆
- 若AB为同阶矩阵,则可逆


求逆矩阵的三个途径:定义、公式、算法





矩阵初等变换

定义2.4.1 (初等变换) 下面三种对矩阵的变换,统称为矩阵的初等变换:
(1) 对调变换:互换矩阵i, j两行(列),记作 ri↔rj (ci↔cj) .
(2) 数乘变换:用任意数k≠0 去乘矩阵的第i行(列),记作kri ( kci ) .
(3) 倍加变换:把矩阵的第i行(列)的k倍加到第j 行(列),其中k为任意数,
记作rj+kri ( cj+kci ) .



矩阵的秩





当秩为1时存在以下特殊结论

线性相关与线性无关




极大无关组





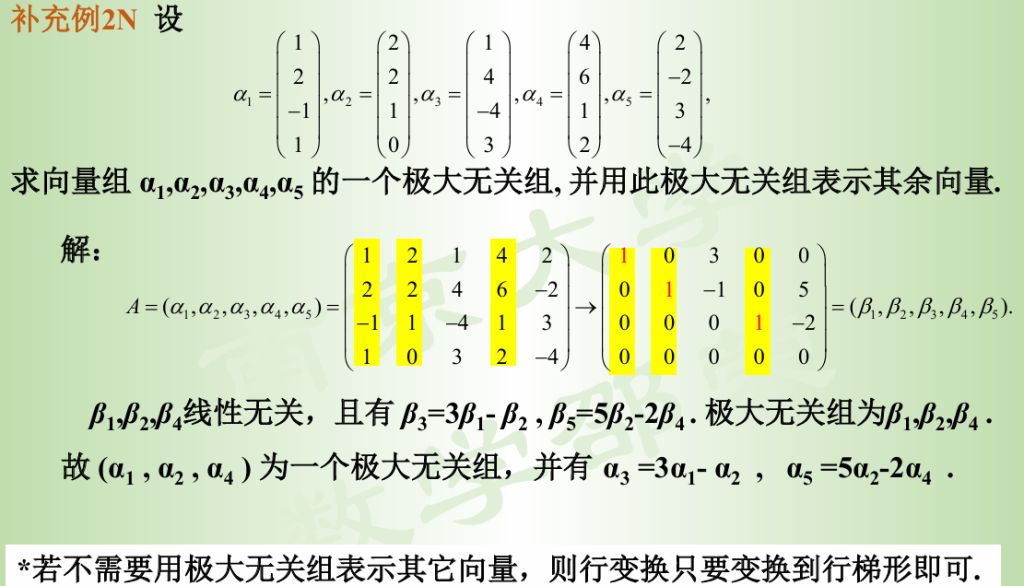
关于向量组的秩的新定义:





线性方程

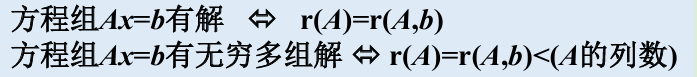
矩阵的构造一例:

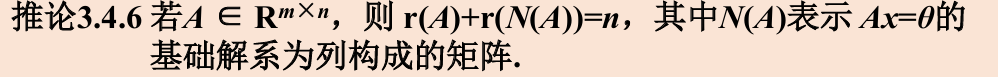

线性相关证明题罗列:


二次型

注意矩阵 A 中对角线上的元素涉及到平方项,斜对角线上的元素涉及到交叉乘积项




正定矩阵(正定二次型)

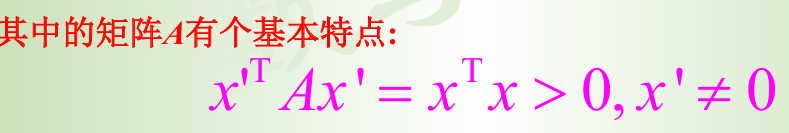
一定要利用好这样的特点,x可以是很多特殊的e向量,也可以是ta+b这样的表示
只要是“实对称矩阵”,都可以试着转换为正定矩阵


正定的另一种证明办法:利用“顺序主子式”


重要第二结论:证明:A为正定矩阵当且仅当A有分解 A=DTD(D可逆)
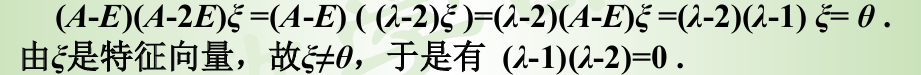
一定要注意这样的式子可以确定所有特征值
六、线性空间
定义6.1.1 (数环) 设R是非空数集,其中任何两个数之和、差与积仍属于R (即R关于加、减、乘法运算是封闭的),则称R是一个数环.
定义6.1.2 (数域) 若K是至少含有两个互异数的数环,且其中任何两数a与b之商(b≠ 0) 仍属于K,则称K是一个数域.
数域是对具有有理数最基本性质的数集合的统称
数域的简单性质:
(1) 数域关于加减乘除(分母不为零)四则运算是封闭的
(2) 任何数域K中必含有0与1
(3) 若a≠ 0,则有1/a=a-1∈K
(重点)关于线性空间的实际定义与证明办法



线性空间的基、维数与坐标


线性空间V中的不同基所含的向量个数相同.
n维线性空间V中的n+1个向量必线性相关,故n个线性无关向量可构成V的一组基.

过渡矩阵的概念


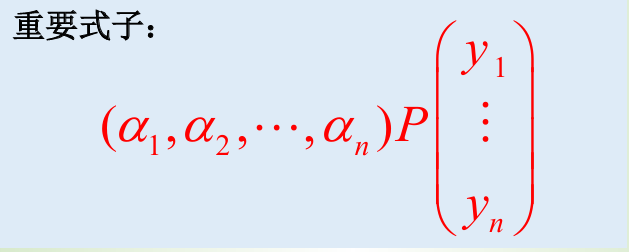
上述式子就是在线性变换之后的坐标表达


