机器学习(NJUSE Machine Learning)
Contents
机器学习概论
机器学习系统
1.人工智能的三大基石:推理、知识、学习(利用经验改善系统的性能)
机器学习的定义
学习是一个蕴含特定目的的知识获取过程,其内部表现为新知识的不断建立和修正,而外部则表现为性能改善。
TIP:经验(数据和常识),在此更多指的是数据,即从数据中总结规律用于将来的预测。

数据层面的数据类型(特点)
- 静态与动态 (如照片与视频等)
- 小数据与大数据 (如异常&正常+类不平衡/代价敏感)
- 同质与异质 (如实数型与符号&实数的混合等)
- 单态与多态 (如仅图像与声音&图像等)
- 小类数与大类数 (如性别与个体识别)
- 缺失&带噪数据
- 高维数据&非数值数据(如串、图等)
经典学习方法
机械学习
归纳学习
类比学习
解释学习
决策树&森林
贝叶斯分类器
聚类
常规术语及其标记
维数灾难
The Curse of Dimensionality in Machine Learning arises when working with high-dimensional data, leading to increased computational complexity, overfitting, and spurious correlations.
简单来讲,维数灾难(或者叫维度诅咒)意思就是:随着输入维数的增加,算法将需要更多的数据,在高维空间中,数据点变得稀疏,由于对空间进行充分采样需要大量数据,因此很难辨别有意义的模式或关系。
The Curse of Dimensionality refers to the phenomenon where the efficiency and effectiveness of algorithms deteriorate as the dimensionality of the data increases exponentially.
一般我们会根据实际情况采取适当的降维处理,保证特征的尽可能保留的前提下丢弃不相干或者冗余的特征,简化模型并且提高效率
数据集
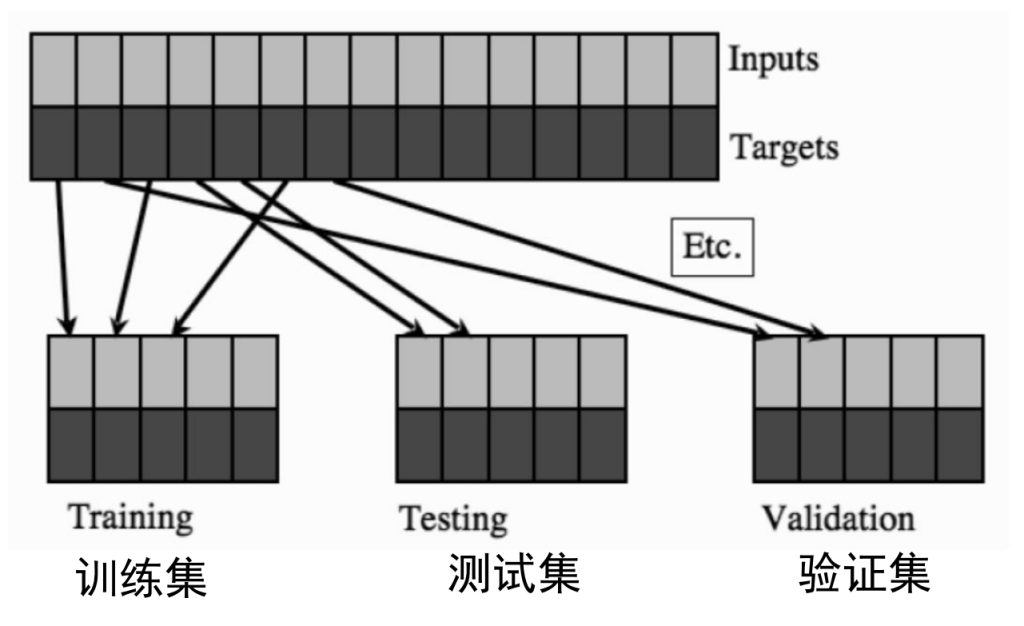
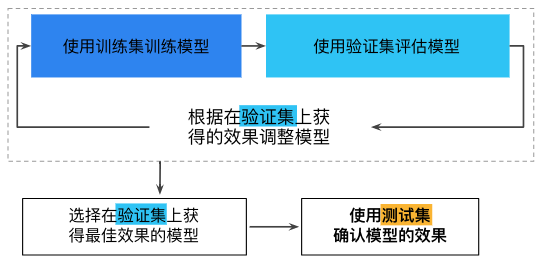
数据集的划分方法:
留出法
留出法(hold-out)直接将数据集划分为互斥的集合,如通常选择 70% 数据作为训练集,30% 作为测试集。
需要注意的是保持划分后集合数据分布的一致性,避免划分过程中引入额外的偏差而对最终结果产生影响。通常来说,单次使用留出法得到的结果往往不够稳定可靠,一般采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
K-折交叉验证法
Kuhn 和 Johnson 在「Data Splitting Recommendations」中指出使用单独的「测试集」(或验证集)具有一定的局限性,包括
- 测试集是对模型的单次评估,无法完全展现评估结果的不确定性。
- 将大的测试集划分成测试集和验证集会增加模型性能评估的偏差。
- 分割的测试集样本规模太小。
- 模型可能需要每一个可能存在的数据点来确定模型值。
- 不同测试集生成的结果不同,这造成测试集具备极大的不确定性。
- 重采样方法可对模型在未来样本上的性能进行更合理的预测。
所以在实际应用中,可以选择 K-折交叉验证(k-fold cross-validation)的方式来评估模型,其偏差低、性能评估变化小。
K-折交叉验证法将数据集划分为 k 个大小相似的互斥子集,并且尽量保证每个子集数据分布的一致性。这样,就可以获取 k 组训练 – 测试集,从而进行 k 次训练和测试。
k 通常取值 10,此时称为 10 折交叉验证。其他常用的 k 值还有 5、20 等。
自助法
自助法(bootstrap method)以自助采样法为基础:每次随机的从初始数据 D 中选择一个样本拷贝到结果数据集 D’ 中,样本再放回初始数据 D 中;这样重复 m次,就得到了含有 $m$ 个样本的数据集 D’。这样就可以把 D’ 作为训练集,而 D\D'作为测试集。这样,样本在 m 次采样中始终不被采集到的概率为
$$\lim_{m\to\infty} (1-\frac{1}{m})^{m} = 1/e = 0.368$$
自助法的性能评估变化小,在数据集小、难以有效划分数据集时很有用。另外,自助法也可以从初始数据中产生多个不同的训练集,对集成学习等方法有好处。
然而,自助法产生的数据集改变了初始数据的分布,会引入估计偏差。因而,数据量足够时,建议使用留出法和交叉验证法。
建模有关要素
· 模型/映射函数f(.)刻画(如线性机, SVM, 神经网络等)
· 确定目标/损失函数(如平方损失, 互熵等,更一般的是凸与非凸)并优化获得模型
· 评测:泛化性能(可解释为举一反三的能力,在未知样本上的预测能力)
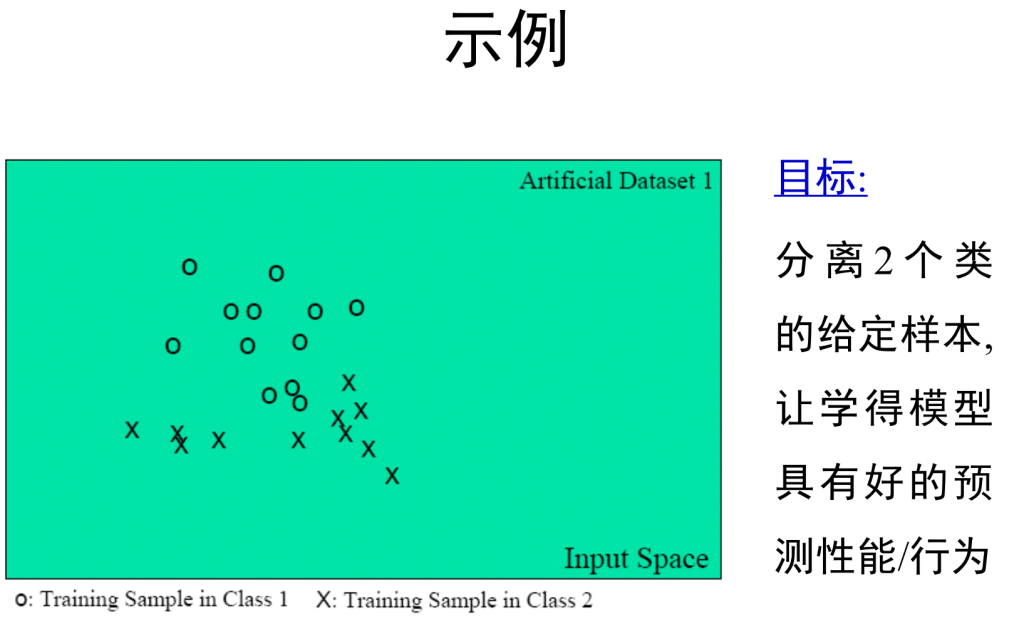
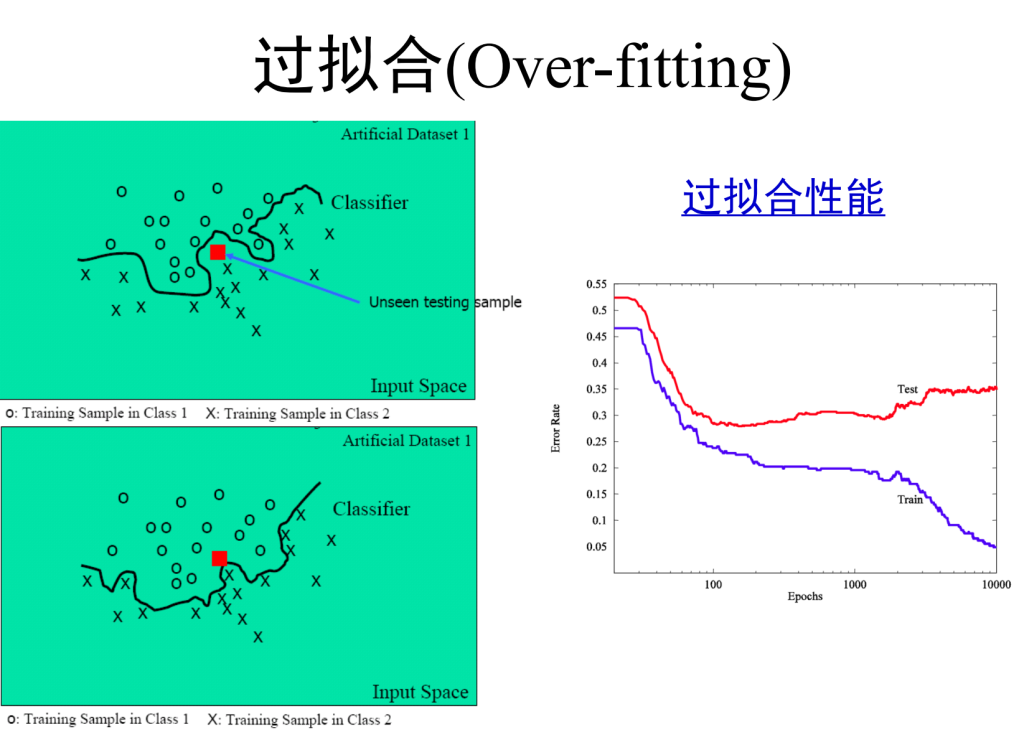
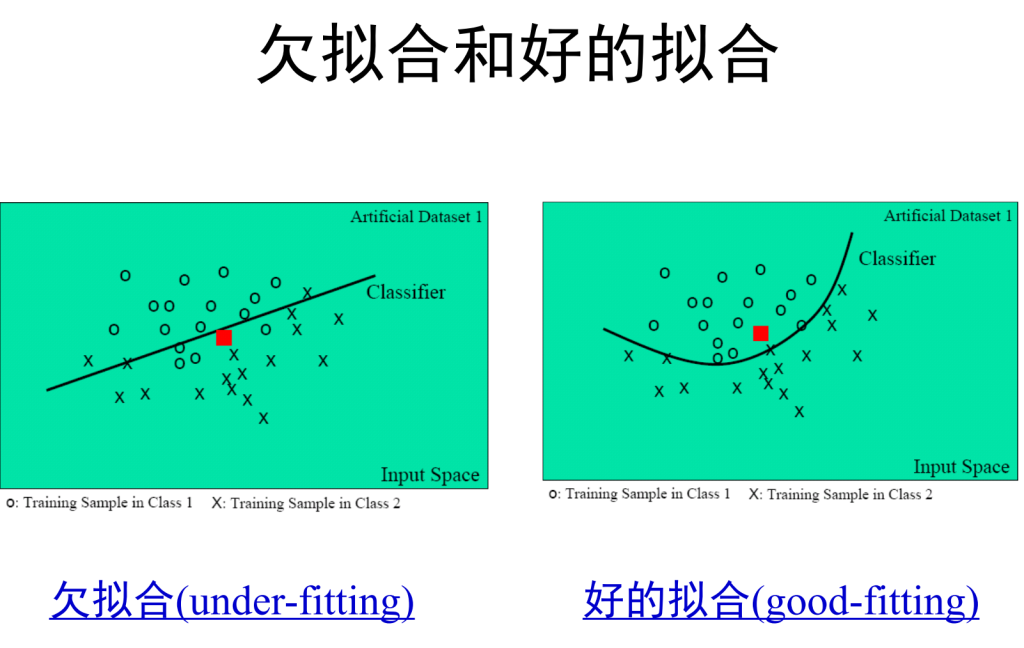
模型选择初探
No Free Lunch Theorem
没有天生优越的学习器,只有充分利用了与问题相关先验知识的模型才是优的!
事实是:
样本(经验)有限,先验甚少,因此从中所建的模型几乎没有一个是对的,只有相对好的!
四类主要方法:模型选择、正则化/规整化、模型组合或集成、多视图方法
机器学习的共性问题

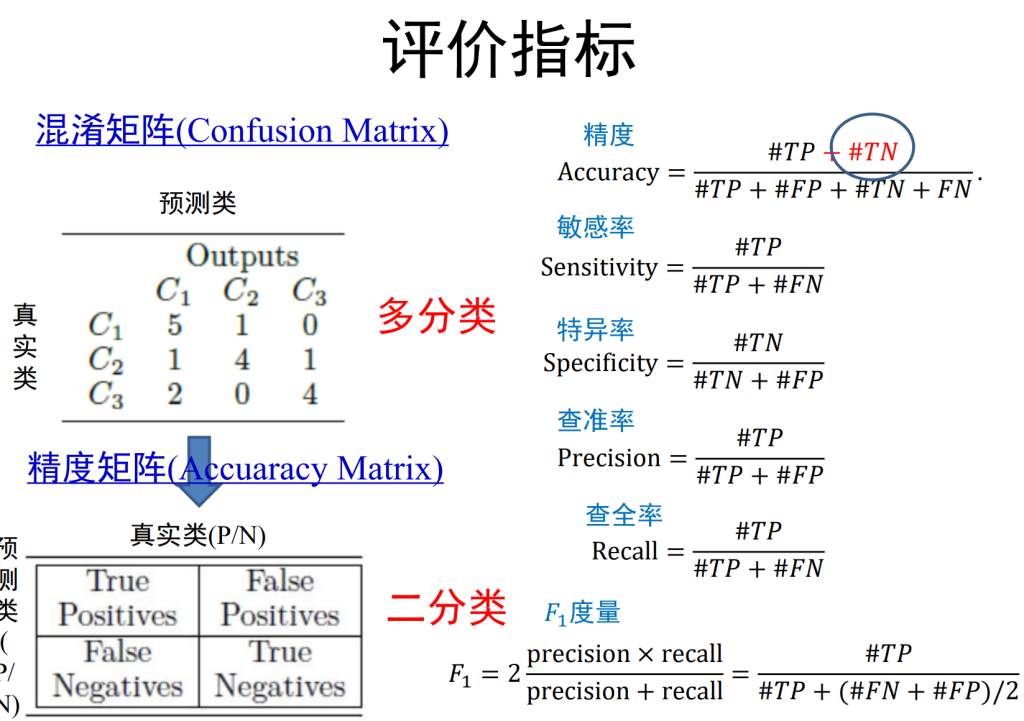
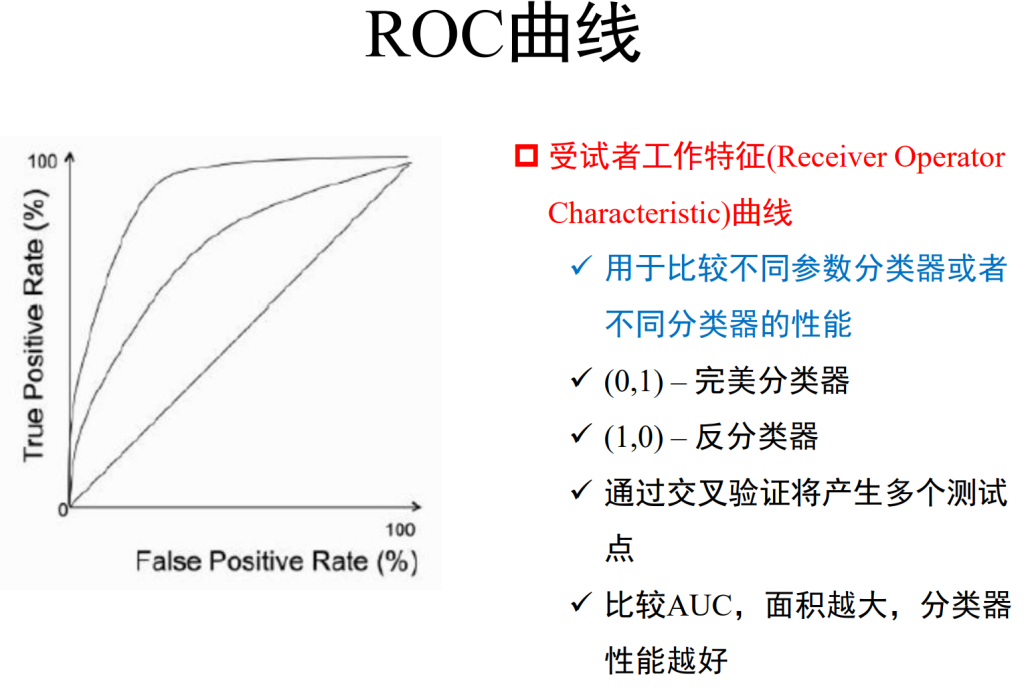

关于测量精度和准确度:

Tikhonov(吉洪诺夫)正则化
1963, Tikhonov 提出了正则化或规整化去解病态问题.
动机
+ 借助某个辅助非负泛函/模型实现解的稳定化!
+ 其中在泛函中嵌入了解或问题的先验信息
如神经网络中权衰减!
在深度网络中用退出(Dropout)! 早期终止,……
丑小鸭定理
没有天生好的特征,只有结合了与问题相关知识的才是好的
Ugly duckling theorem – Wikipedia
丑小鸭定理是一个论点,表明如果没有某种偏见(bias),分类是不可能的。更具体地说,它假设了可通过逻辑连接词组合的有限许多属性,以及有限许多对象;它断言任何两个不同的对象共享相同数量的 (扩展) 属性
统计学基本概念

【数学】方差、协方差、协方差矩阵 – LENMOD – 博客园 (cnblogs.com)
线性模型
数据的线性可分性
线性可分指的是可以用一个线性函数将两类样本分开(注意这里是线性函数),比如在二维空间中的直线,三位空间中的平面以及高维空间中的超平面。这里指的可分是没有一丝误差的分开,线性不可分指的就是部分样本用线性分类面划分时会产生分类错误的现象。
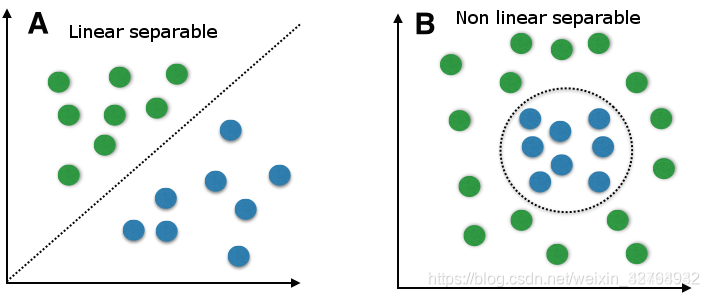
可以采用凸包是否相交的办法来判断,o r直接是否存在n+1个变量,使得所有属于X0和X1的 变量满足
$$
\sigma_{i=1}^{n}{w_ix_i}>k
$$
线性模型
在乘法式子中的系数w,如果只对一个变量存在影响,那么这个模型就是线性模型,y=w0+w1*x这种
决策树
A decision tree is a decision support hierarchical model that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements.
决策树基于其“树”的结构进行决策,每个“内部节点”对应于某个属性的测试,而每个分支对应于该测试的一种可能结果
基本流程:
采取分而治之的方式,自根至叶的递归过程,在每个中间节点寻找“划分”的属性
终止条件:当前节点包含样本全部属于同类别;当前属性集为空or全相同,无法划分;当前节点包含样本集合为空,不能划分

信息增益方法选取划分属性

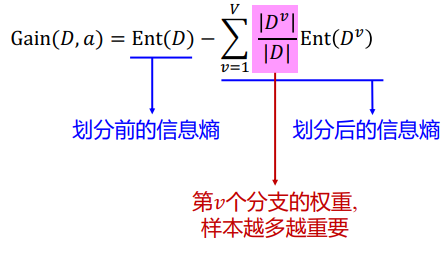

具体某个节点的信息熵都可以用“正例反例”来作为划分计算
最后选择信息增益最大的属性作为划分属性,对每个分支结点做进一步划分,最终得到决策树
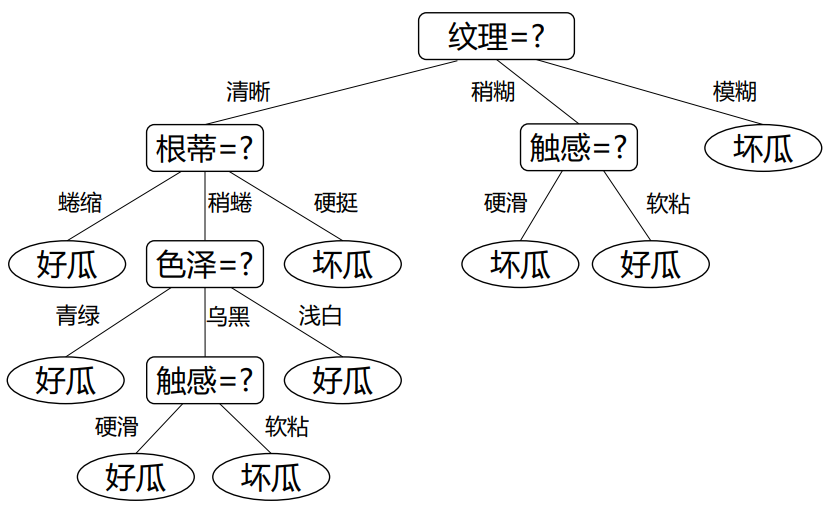
与此对应还有“增益率”算法,信息增益的表达采取“增益率”的办法来解决

但信息熵的方式采取的事对数计算,具有比较大的计算复杂度,因此还有别的办法:即基尼系数计算

在候选属性集合中,选取那个使划分后基尼指数最小的属性
决策树优化
划分选择的各种准则虽然对决策树的尺寸有较大影响,但对泛化性能
的影响很有限
因此需要采取别的办法处理泛化,这里到了一个常用算法:剪枝
剪枝 (pruning) 是决策树对付“过拟合”的主要手段!
剪枝主要理论
基本策略:
- 预剪枝 (pre-pruning) : 提前终止某些分支的生长
- 后剪枝 (post-pruning): 生成一棵完全树,再“回头”剪枝
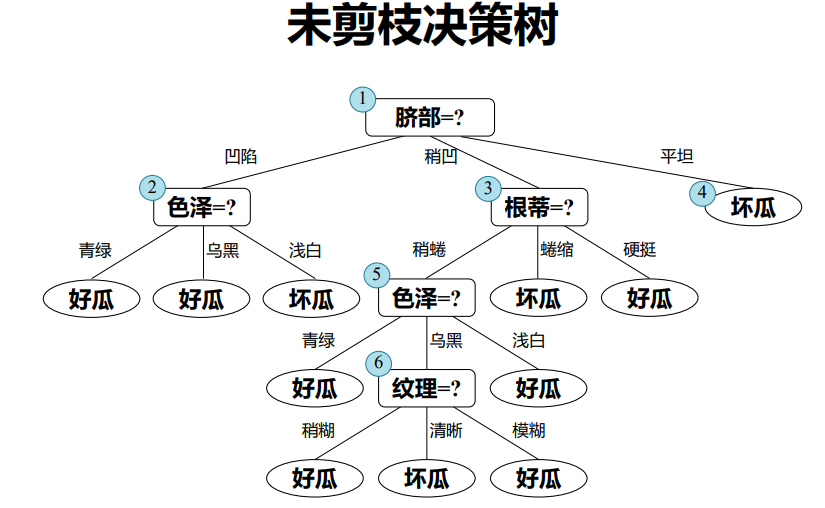
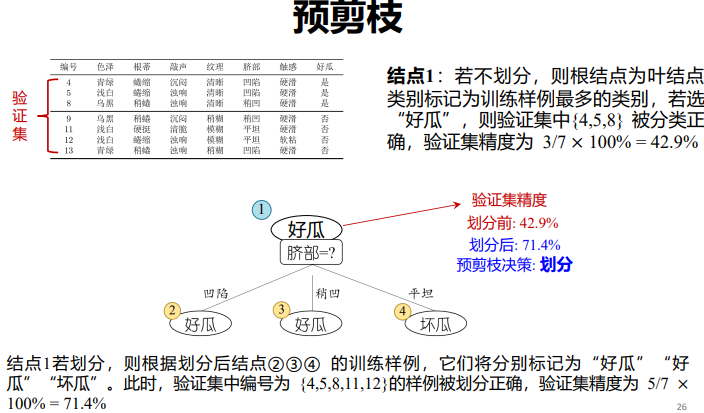
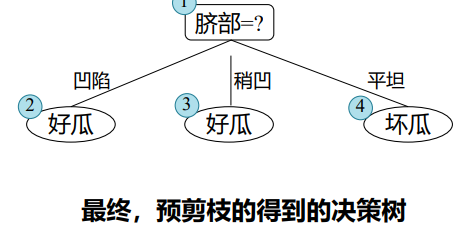
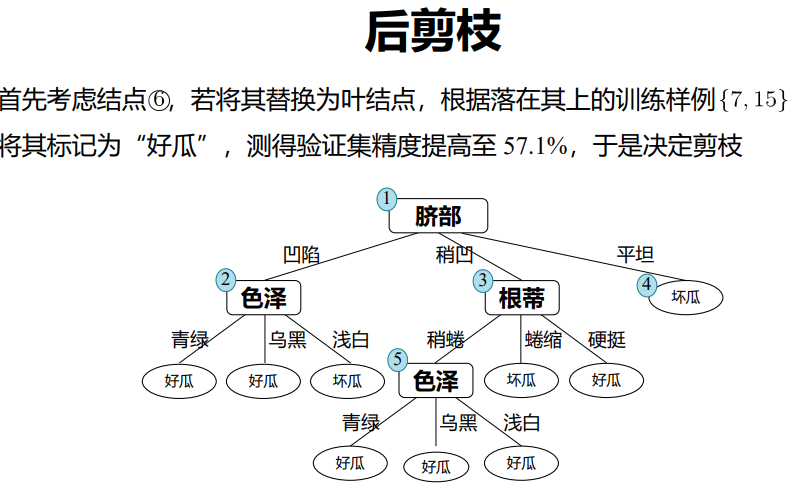
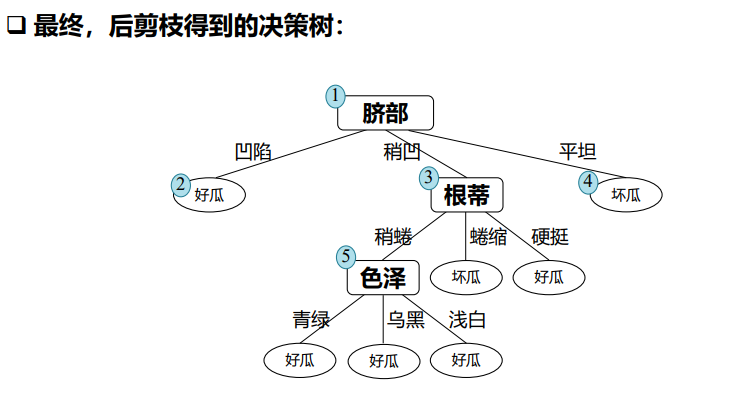
预剪枝:测试时间开销降低,训练时间开销降低
后剪枝:测试时间开销降低,训练时间开销增加
过/欠拟合风险:
- 预剪枝:过拟合风险降低,欠拟合风险增加
- 后剪枝:过拟合风险降低,欠拟合风险基本不变
特殊值决策
连续值

缺失值



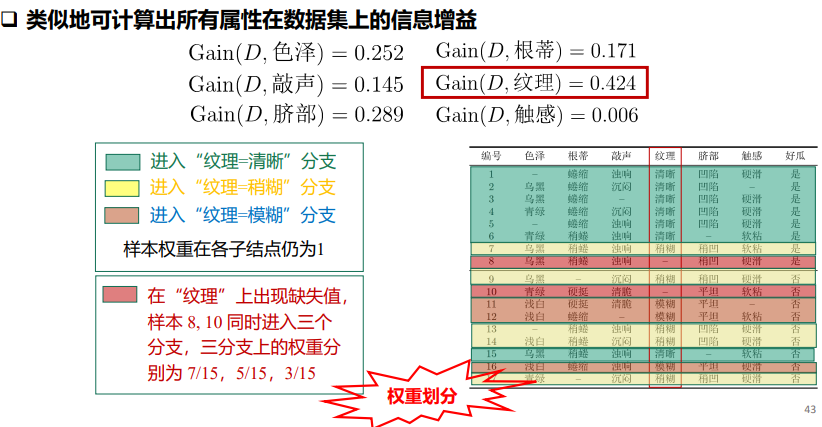
extension
K-近邻算法
回顾

可用的距离度量:

一些特征:
欧几里得距离(Euclidean Distance):计算两个点在n维空间中的直线距离。它是最常用的距离度量,适用于连续变量。
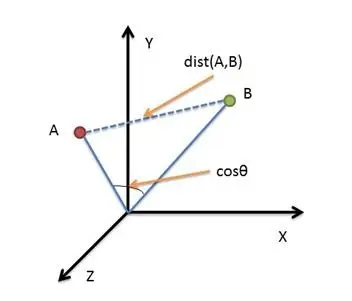
余弦相似度(Cosine Similarity):计算两个向量的夹角,常用于文本数据的相似性比较,忽略向量的大小。
曼哈顿距离(Manhattan Distance):计算两个点在n维空间中沿坐标轴的距离,适用于网格状布局的场景。
切比雪夫距离(Chebyshev Distance):取每个维度上的最大差异,适用于棋盘格状布局的场景。
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。

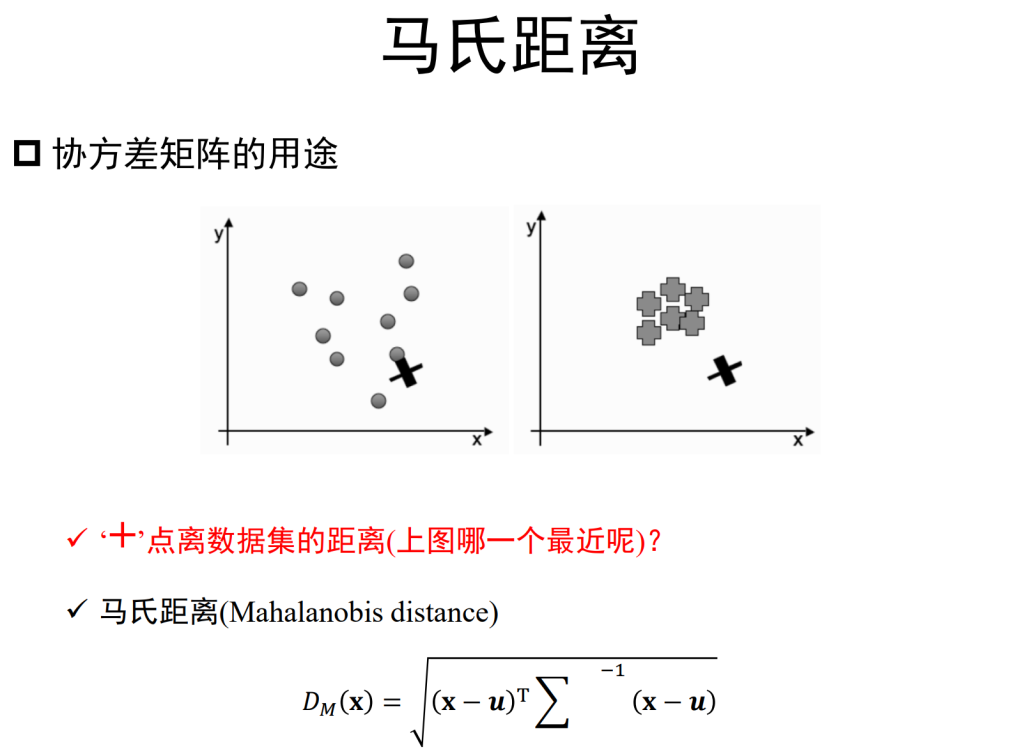
马氏距离(Mahalanobis Distance):上图有两个正态分布的总体,它们的均值分别为a和b,但方差不一样,则图中的A点离哪个总体更近?或者说A有更大的概率属于谁?显然,A离左边的更近,A属于左边总体的概率更大,尽管A与a的欧式距离远一些。这就是马氏距离的直观解释。
马氏距离是基于样本分布的一种距离。物理意义就是在规范化的主成分空间中的欧氏距离。所谓规范化的主成分空间就是利用主成分分析对一些数据进行主成分分解。再对所有主成分分解轴做归一化,形成新的坐标轴。由这些坐标轴张成的空间就是规范化的主成分空间。
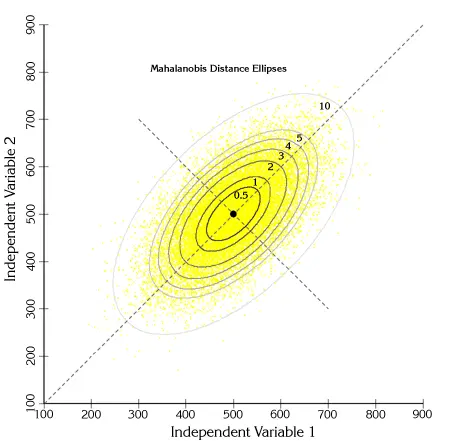
马氏距离的计算是建立在总体样本的基础上的,如果拿同样的两个样本,放入两个不同的总体中,最后计算得出的两个样本间的马氏距离通常是不相同的,除非这两个总体的协方差矩阵碰巧相同;


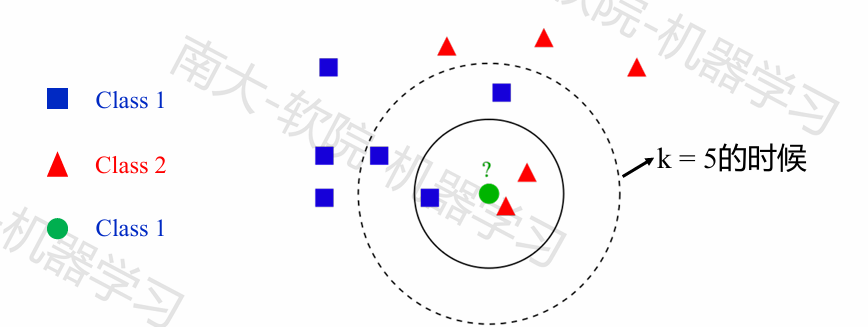

结论:最近邻分类器虽然简单,但它的泛化错误率不超过贝叶斯分类器的错误率两倍!

一般情况下,最近邻分类器效果比最简单的贝叶斯分类器效果好

以上介绍了贝叶斯分类器中的概念,

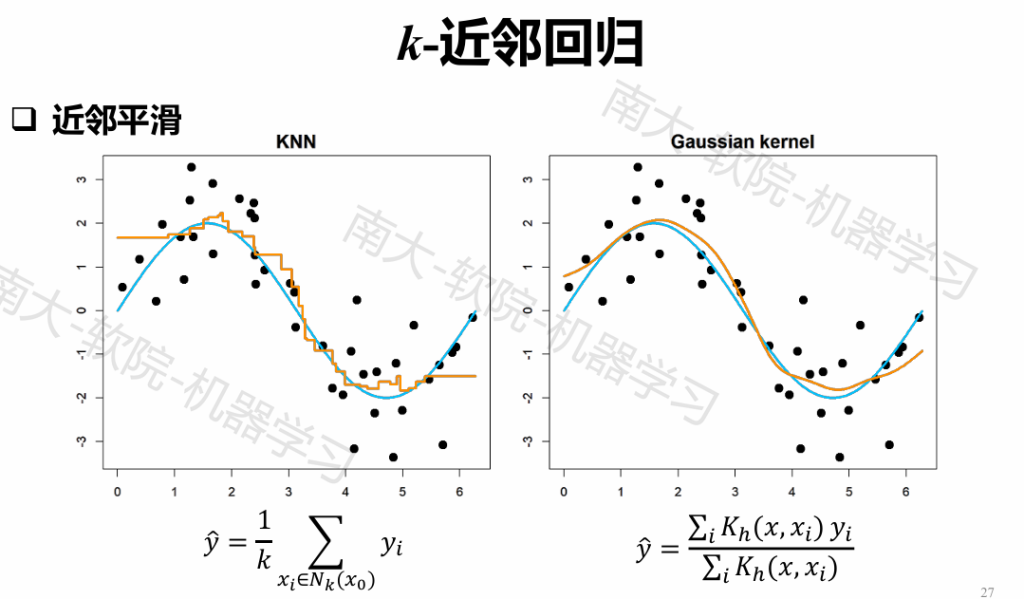
近邻平滑


降低近邻计算
定义:根据一组给定的目标,将一个平面划分成靠近每一个目标的多个区块
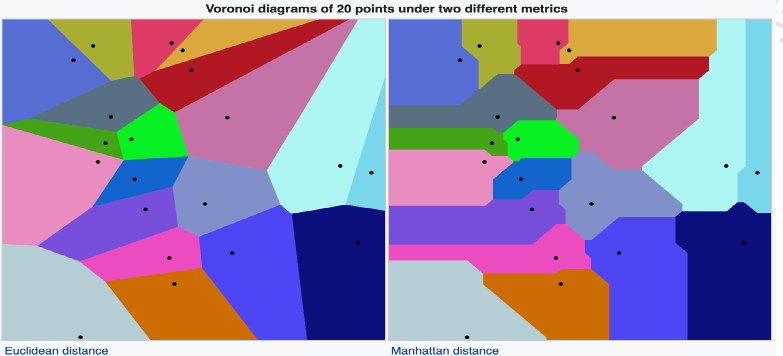
维诺图由一系列维诺单元(Voronoicells)组成,假设𝑋是一个点集,包含𝐾个基点(𝑃) ∈,那么维诺单元𝑅定义为:
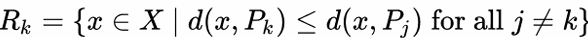

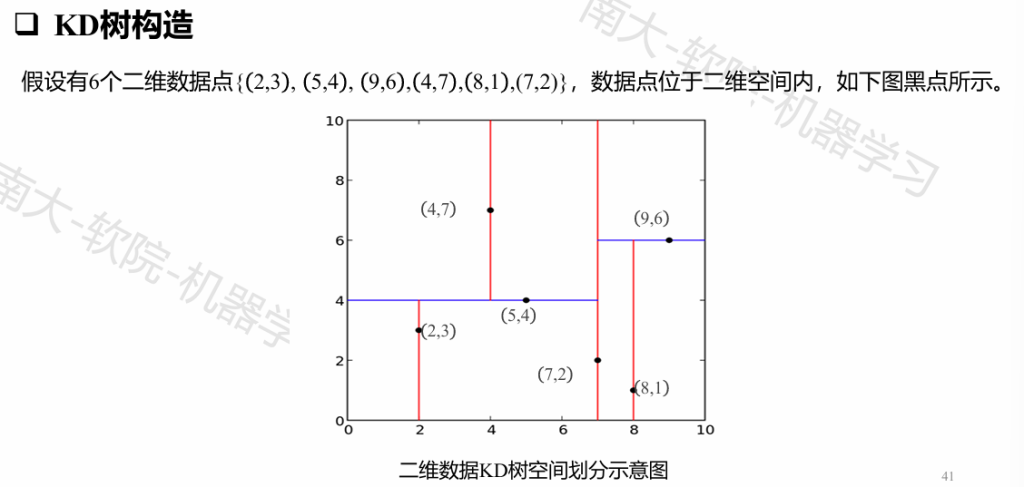
KD-Tree
KD树是一种对K维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。
KD树是二叉树,表示对K维空间的一个划分(partition)。构造KD树相当于不断地用垂直于坐标轴的超平面将K维空间切分,构成一系列的K维超矩形区域。KD树的每个结点对应于一个K维超矩形区域



无监督学习和聚类算法

比如我们既可以从颜色去对这些几何图形分类,但是基于形状分类也是有道理的
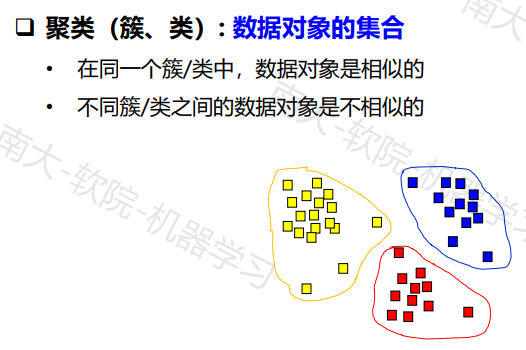

聚类的依据
- 将整个数据集中每个样本的特征向量看成是分布在特征空间中的一些点,
点与点之间的距离即可作为相似性度量依据 - 聚类分析是根据不同样本之间的差异,根据距离函数的规律(大小)进行
聚类的



聚类准则函数方法

基于试探的聚类搜索算法

在实际中,对于高维样本很难获得准确的先验知识,因此只能选用不同的
阈值和起始点来试探,所以这种方法在很大程度上依赖于以下因素:
- 第一个聚类中心的位置
- 待聚类样本的排列次序
- 距离阈值T的大小
- 样本分布的几何性质

系统聚类法

主要的距离计算准则:
➢ 最短距离法 (两个集合所有距离最小值)
➢ 最长距离法 (两个集合所有距离最大值)
➢ 类平均距离法(两个集合所有距离平均值)
动态聚类法
基本思想
- 首先选择若干个样本点作为聚类中心,再按某种聚类准则(通常采用最小
距离准则)使样本点向各中心聚集,从而得到初始聚类; - 然后判断初始分类是否合理,若不合理,则修改聚类
- 如此反复进行修改聚类的迭代算法,直至合理为止。
K-means算法
算法流程
- Step1:选择一个聚类数量 k
- Step2:初始化聚类中心 1,… ,k
- 随机选择𝑘个样本点,设置这些样本点为中心
- Step3:对每个样本点, 计算样本点到𝑘个聚类中心的距离(使用某种距离度量),
将样本点分距离它最近的聚类中心所属的聚类 - Step4:重新计算聚类中心,聚类中心为属于这一个聚类的所有样本的均值
- Step5:如果没发生样本所属的聚类改变的情况,则退出,否则,返回Step3继续
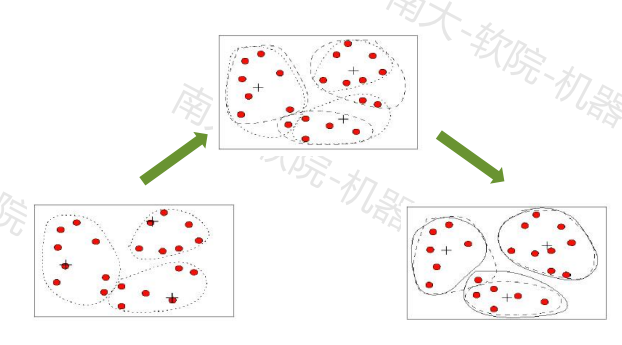
改进:K-means++算法

ISODATA算法(Iterative Self-organizing Data Analysis Techniques)
基本步骤和思路
- (1)选择某些初始值。可选不同的参数,也可在迭代过程中人为修改,以将N个样本按指标分配到各个聚类中心中去。
- (2)计算各类中诸样本的距离指标函数。
- (3)~(6)按给定的要求,将前一次获得的聚类集合进行分裂和合并处理,(5)为分裂处
理,(6)为合并处理,从而获得新的聚类中心。 - (7)重新进行迭代运算,计算各项指标,判断聚类结果是否符合要求。经过多次迭代后,若
结果收敛,则运算结束。

支持向量机



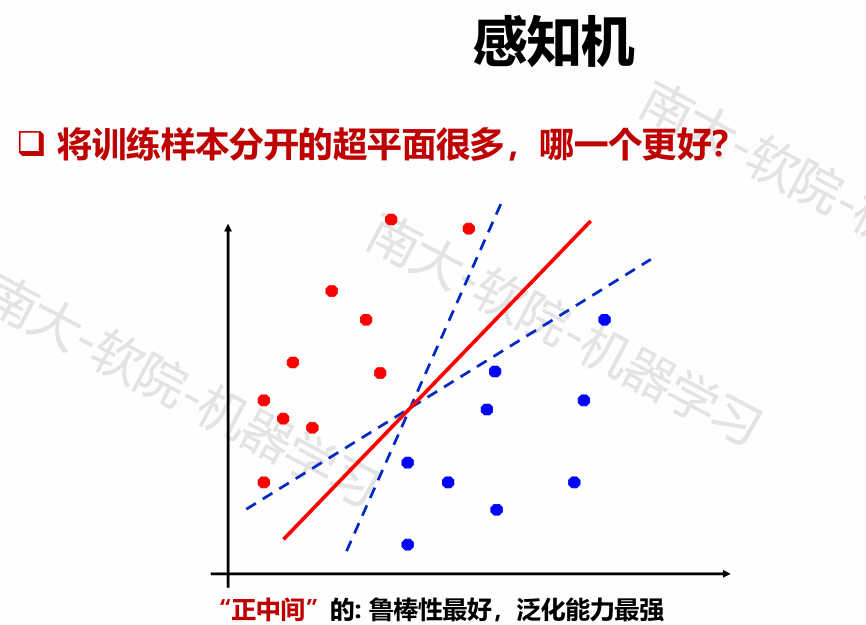
一个点(样例)对应的“间隔”margin是其到分界超平面的垂直距离
具有最小间隔的点称为支持向量(support vectors)
支持向量机(英语:support vector machine,常简称为SVM,又名支持向量网络)是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例,每个训练实例被标记为属于两个类别中的一个或另一个,SVM训练算法创建一个将新的实例分配给两个类别之一的模型,使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点,这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后,将新的实例映射到同一空间,并基于它们落在间隔的哪一侧来预测所属类别。
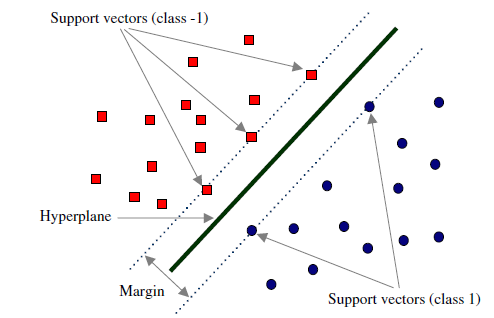
- 线性可分SVM
- 当训练数据线性可分时,通过硬间隔(hard margin,什么是硬、软间隔下面会讲)最大化可以学习得到一个线性分类器,即硬间隔SVM,如上图的的H3。
- 线性SVM
- 当训练数据不能线性可分但是可以近似线性可分时,通过软间隔(soft margin)最大化也可以学习到一个线性分类器,即软间隔SVM。
- 非线性SVM
- 当训练数据线性不可分时,通过使用核技巧(kernel trick)和软间隔最大化,可以学习到一个非线性SVM。
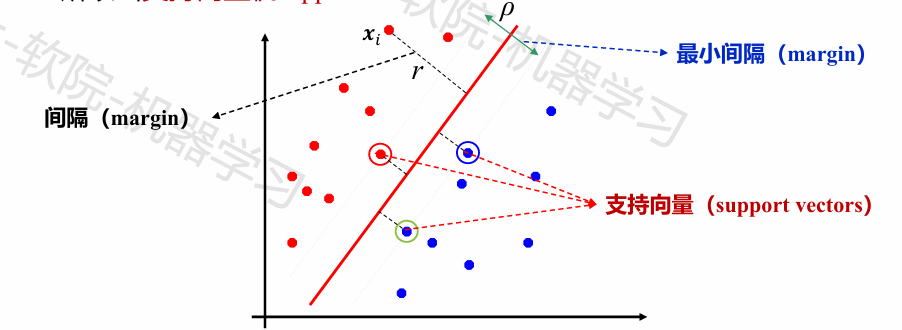
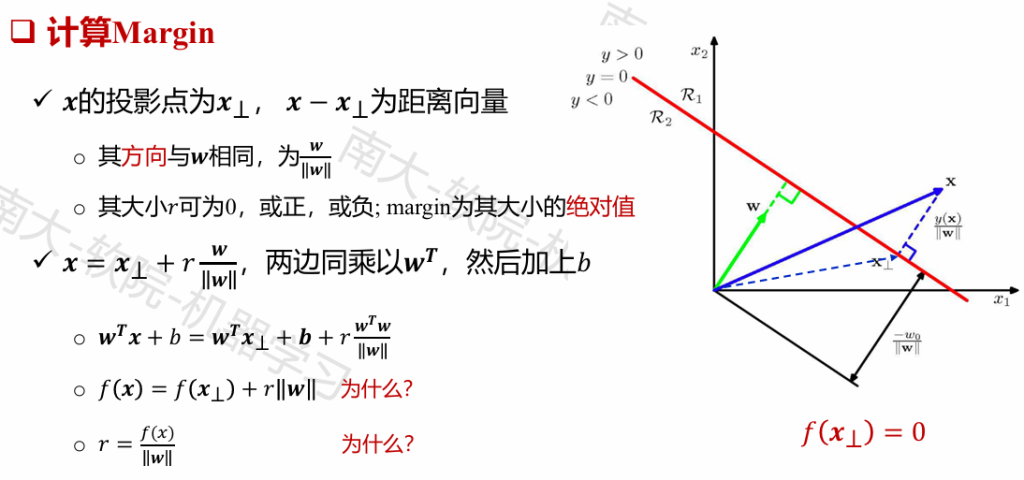

对𝑤没有限制,要求最大化最小的间隔,难优化

我们限定min𝑦(𝒘𝑻𝒙+𝑏) 为1,不改变最优目标值

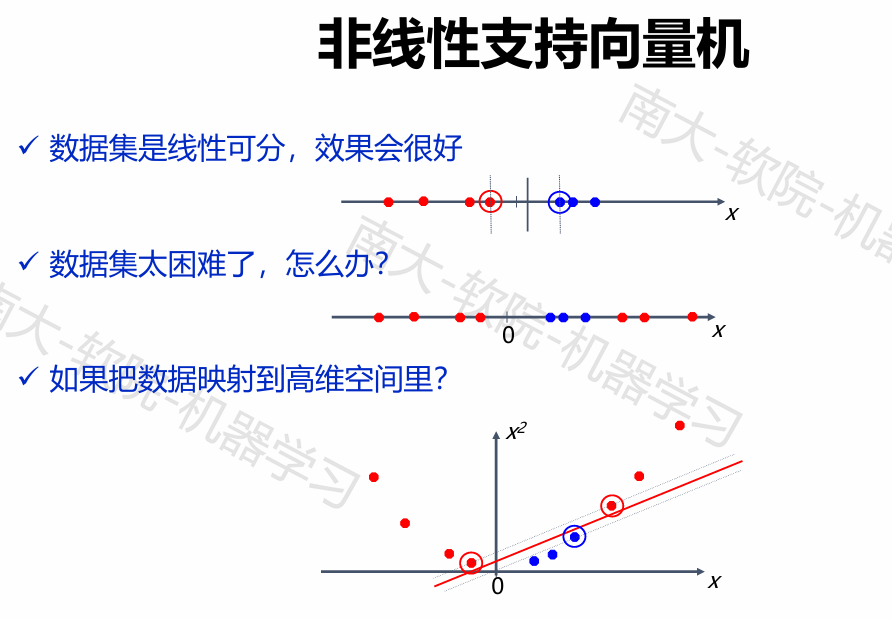
如果原始空间是有限维(属性数有限),那么一定存在一个高维特征空间使样本可分
感知机
神经网络
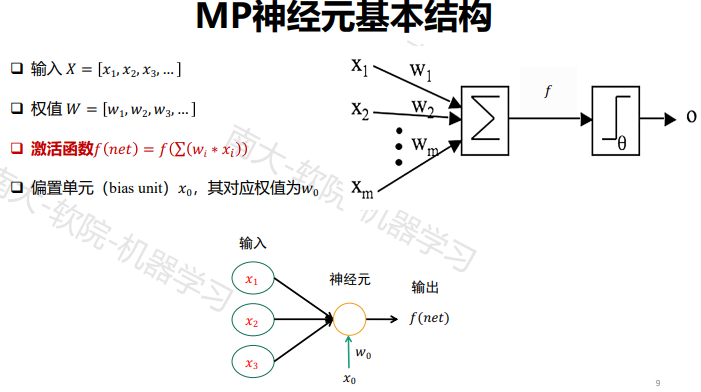
ü 一组输入加权wi相当于突触
ü 一个加法器把输入信号相加(与收集电荷的细胞膜等价)
ü 一个激活函数(最初是一个阈值函数)决定细胞对于当前的输入是否激活(“放电”)

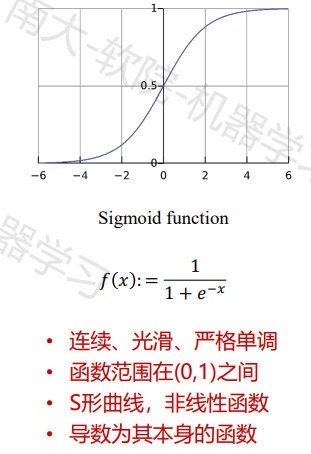
常见激活函数


感知机
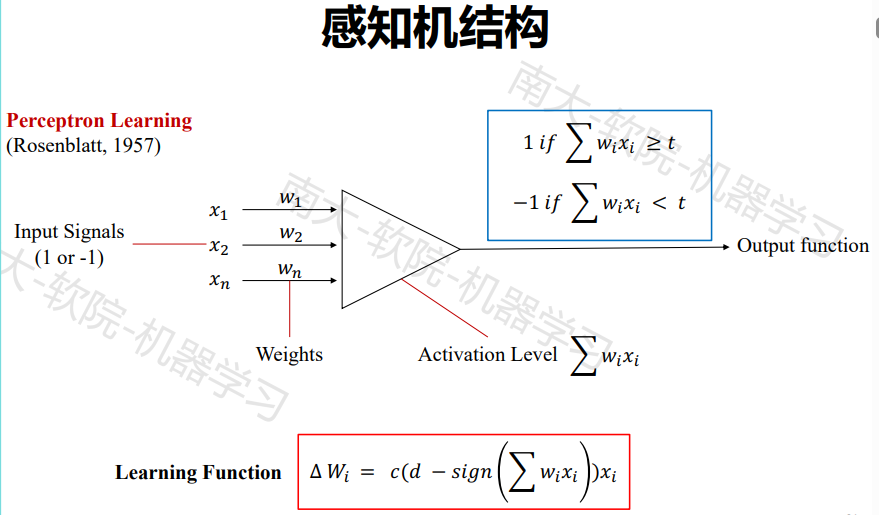
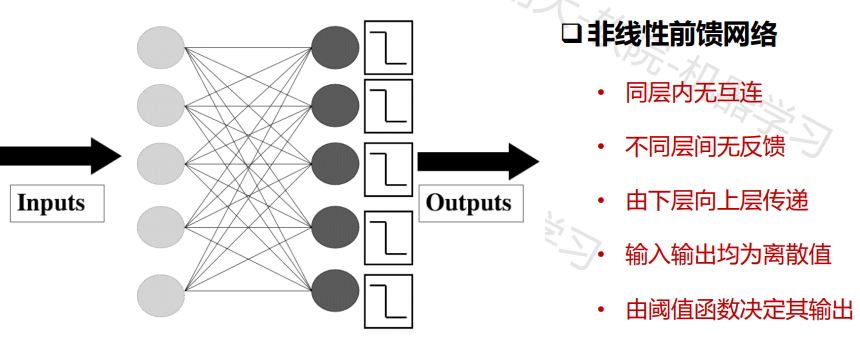

感知机的学习算法
- 权值初始化
- 输入样本对
- 计算输出
- 根据感知机学习规则调整权重
- 返回步骤2,输入下一对样本,直至对所有样本的实际输出
与期望输出相等
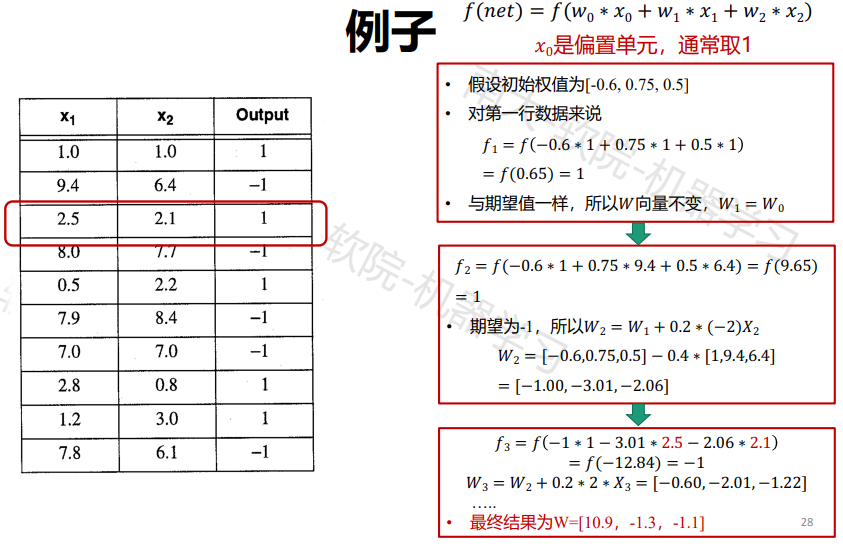
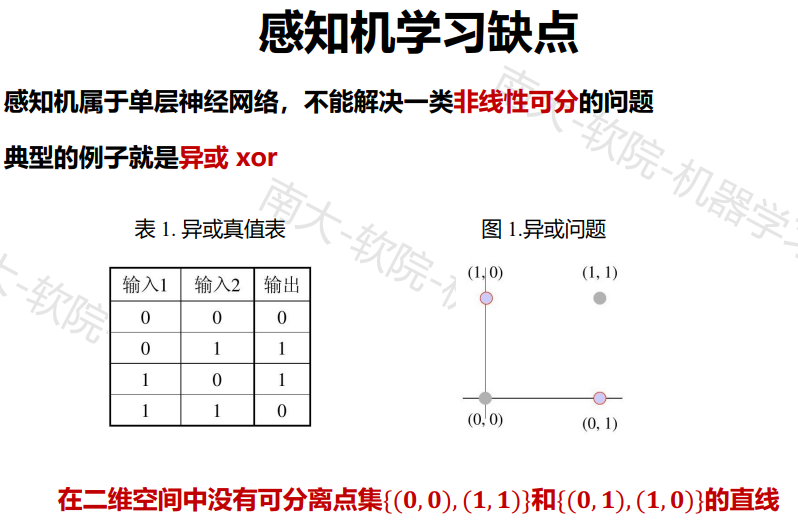
多层神经网络
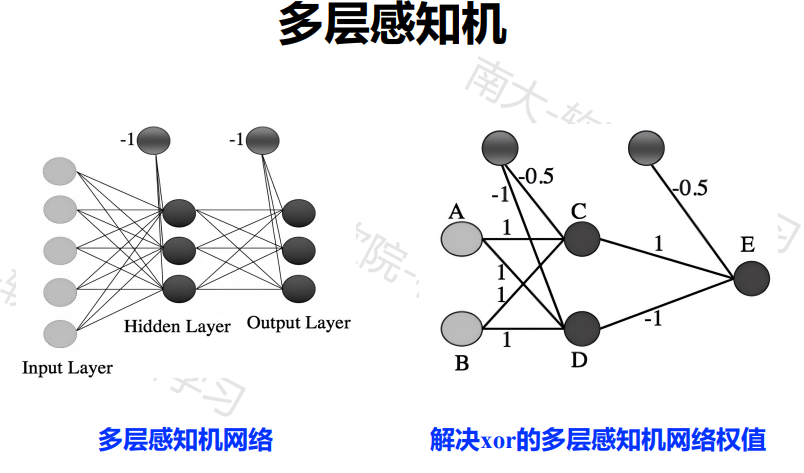
隐藏层神经元实际为特征检测算子(feature detector),在多层神经网络的学习过程中,隐藏层神经元开始逐步“发现”,刻画训练数据的突出特征
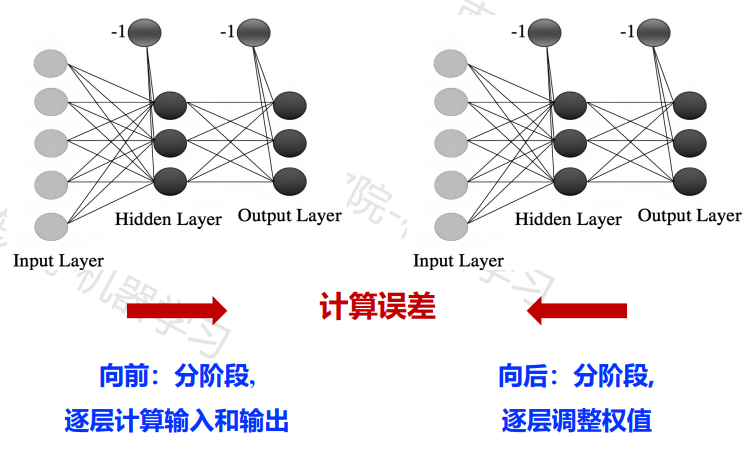
多层网络:包含隐层的网络前馈网络:神经元之间不存在同层连接也不存在跨层连接
BP神经网络算法:迄今最成功、最常用的神经网络算法,可用于多种任务(不仅限于分类
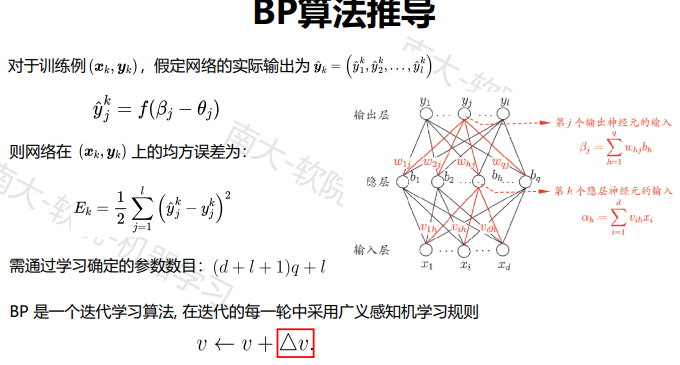
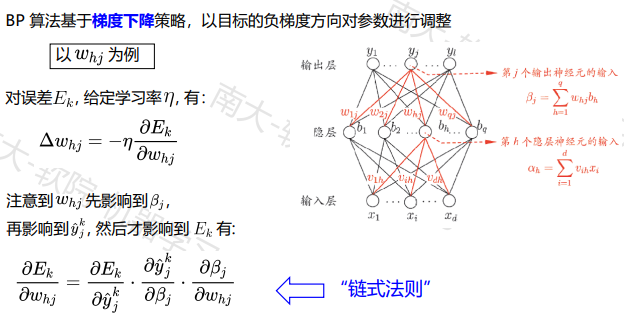
此处注意学习率的调节,太大太小都不行

如何缓解过拟合:

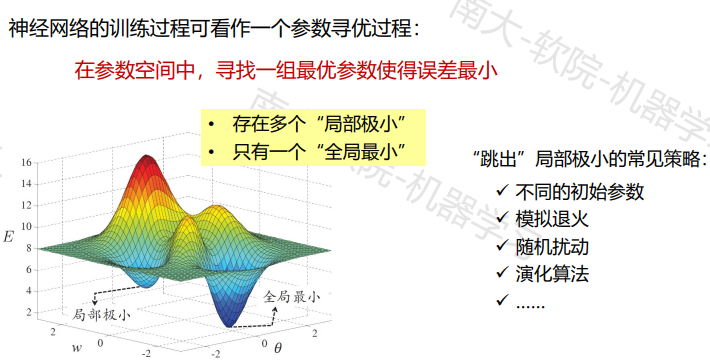
维度约简
概率学习
优化和搜索
演化学习
强化学习
贝叶斯分类器
贝叶斯分类器是一种基于生成式模型的分类器,其基本思想是利用贝叶斯公式计算后验概率 p(y|x),然后选择使得后验概率最大的类别作为预测结果。
两种机器学习的策略
机器学习所要实现的目标在某种程度上可以视作利用有限的样本进行学习,以达到给定输入 x,尽可能准确地预测后验概率 p(y|x) 的目标。由于 p(y|x) 是未知的,因此主要有两种策略:
生成式模型:对联合分布 p(x,y) 进行建模,然后通过贝叶斯公式计算后验概率 p(y|x)。
判别式模型:直接对 p(y|x) 进行建模,例如决策树、支持向量机、神经网络等。
贝叶斯公式
给定样本 x 和类别 c,贝叶斯公式为:
$$p(c|\mathbf{x}) = \frac{p(\mathbf{x}|c)p(c)}{p(\mathbf{x})}$$
其中 p(c|x) 是后验概率,也是我们的目标;p(x|c) 是似然度,表示在类别 c 下样本 x 出现的概率;p(c) 是先验概率,表示类别 c 出现的概率;p(x) 是证据因子,是与类别无关的因子。
贝叶斯决策论

极大似然估计
在实际应用中,我们通常先假设似然 P(x|c) 有某种概率的分布形式(这种分布形式带有参数,而概率分布可被参数 θc 唯一确定),然后再根据训练样例对参数进行估计。
θc 对于训练集 D 中的类别 c,可以通过极大似然估计得到:
$$P(D_{c}|\theta_{c}) = \prod_{i=1}^{N} P(\mathbf{x}_{i}|c, \theta_{c})$$
一般使用对数似然来简化计算并避免数值下溢:
$$
\theta_{c} = \arg\max_{\theta} \log P(D_{c}|\theta_{c})$$
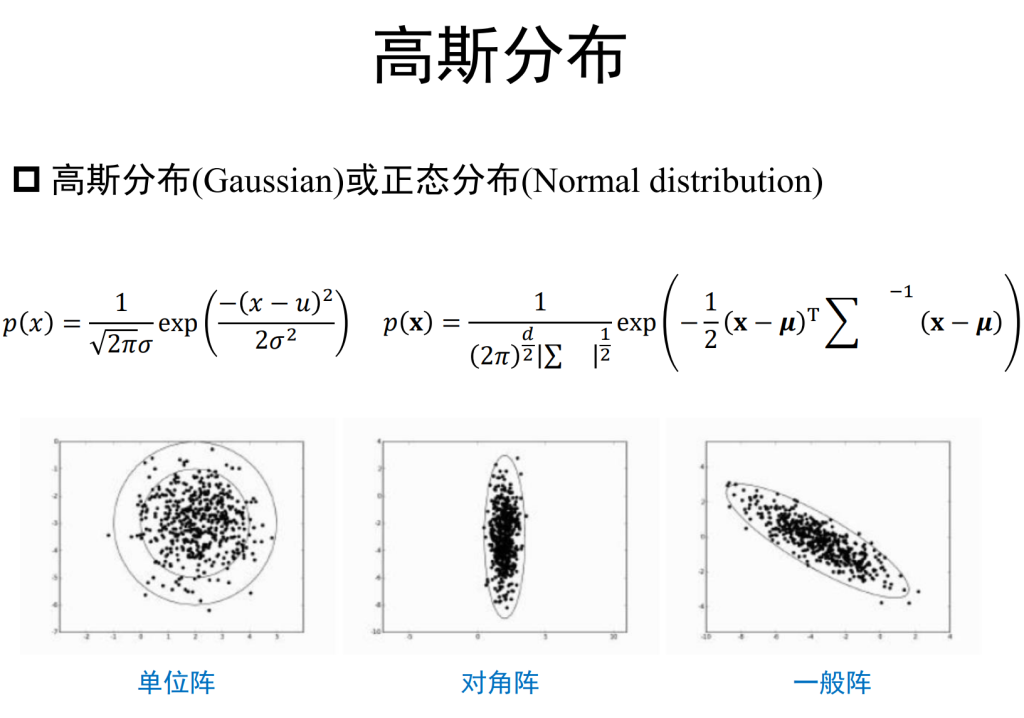
例如,如果假设 P(x|c) 服从高斯分布,即 P(x|c)∼N(μc,Σc2),则可以通过最大似然估计得到(其中 N 为训练集中类别 c 的样本数):

