体积光渲染

1什么是体积光?
在现实环境中,我们有时候会看到光路从云之间洒下来,在带有一些烟雾的舞台上可以看到聚光灯下具有“体积”的光,这种现象名为丁达尔效应Tyndall effect,又称丁达尔现象、延得耳效应(也被广大网友玩梗无数称作各种XXX效应,如达尔文效应等),其原理是光被悬浮的胶体粒子散射。下图中德国宫廷主教座堂内被散射而显现的光路,是丁达尔效应的一个典型例子。

这里有非常明显的效应产生,即光线遇到细小颗粒发生了相当多次的散射
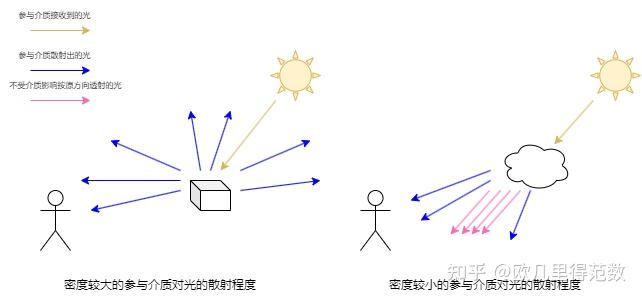
光在介质中传播,会受以下四种因素而发生改变:
- Absorption,光线被物质吸收并由光能转化为其他能量
- Out-scattering,光线被介质中的微粒向外散射
- Emission,介质由于黑体辐射等因素产生自发光
- In-scattering,从其他地方散射到当前光路上的光线

其中,介质对光线的吸收和散射会影响光线在介质中的透射率 (transmittance)。
我们可以用下式来描述一个点光源发出的光线在介质中的散射效果:
$$
L_i(c,v) = T_r(c,p)L_o(p,v)+ \int^{||p-c||}_{t=0}T_r(c,c-vt)L_{scat}(c-vt,v)\sigma_sdt
$$
其中的Lr表示的是介质中某一位置 x 到摄像机位置 c 的光线透射率函数,Lscat表示的是介质中 x 点向视线方向 v 的散射光
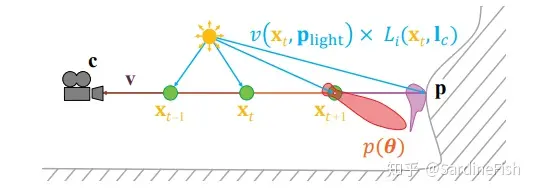
Transmittance
光线在介质中两点 𝑥𝑎,𝑥𝑏 间的透射率可以用下式描述
$$
T_r(x_a,x_b) = e^{-\tau}
$$
其中
$$
\tau = \int^{x_b}_{x=x_a}\sigma_t(x)||dx||
$$
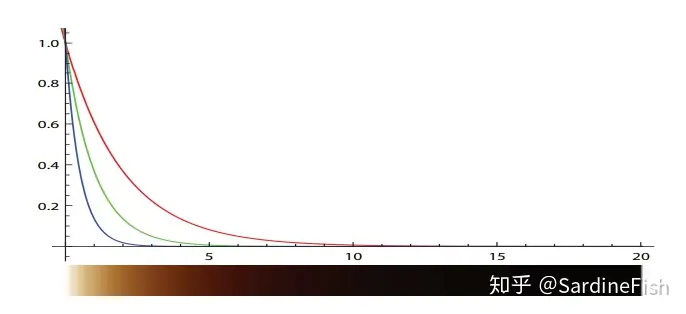
该式又被称为 Beer-Lambert Law,σx代表的事x处对光线的衰减率,包括吸收和向外散射,即transmittance = absorb + scattering
τ被称为 optical depth,表示最终对光线的衰减量,没有单位。在该式下,越高的衰减率或者更长的距离,都会使得 optical depth 增大,并得到更低的光线透射率。σt 可以具有 RGB 分量,例如下图是 σt = (0.5, 1.0, 2.0) 的介质中的光线透射率与透射距离的关系,以及表现出来的散射颜色。
Scattering
在介质中的 x 处,从点光源发出的光线散射到 v 方向上的光,可以通过下式表述
$$
L_{scat}(x,v) = \pi \sum_{i=1}^np(v,l_{c_i})v(x,p_{light_i})c_{light_i}(||x-p_{light_i}||)
$$

phase function
phase function 用于描述在宏观上光线在介质中经过散射到各方向上的概率分布,通常表示为入射与出射光线夹角 θ 的函数 p(θ). 因为能量守恒,phase function 在单位球上的积分必须等于1
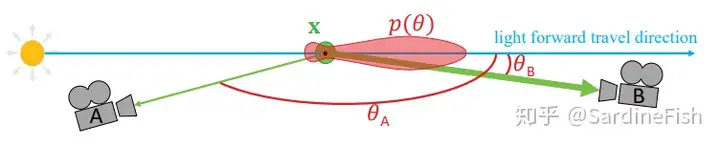

- 对于相对(光的波长)尺寸很小的粒子,发生瑞利散射,比如空气。
- 对于相对尺寸接近1的粒子,发生米氏散射,常见的粒子为雾中的聚光灯、太阳方向上的云,也就是体积光对应的Phase function。
- 当粒子尺寸明显大于光线波长,发生几何散射。
Rayleigh Scattering
$$
p(\theta) = \frac{3}{16\pi}(1+\cos^2\theta)
$$
Mie Scattering (Henyey-Greenstein phase function) [3]
$$
p_{hg}(\theta,g) = \frac{1-g^2}{4\pi(1+g^2-2g\cos\theta)^{1.5}}
$$
式中参数 g 影响散射光在顺光或逆光方向上的相对强度,取值范围 [-1, 1]。Blasi 提出了该式的快速近似实现(又常称为 Schlick phase function)
$$
p(\theta,k) = \frac{1-k^2}{4\pi(1+k\cos\theta)^2} \approx 1.55g – 0.55g^2
$$
Geometric Scattering
当介质中微粒显著大于光的波长时,光线将会发生折射与反射,要从宏观上模拟这样的散射现象,通常需要非常复杂的散射模型,例如体积云的渲染
实时的体积光渲染方案
Volumetric Data
体积渲染中材质的一个重要属性是 transmittance 函数中的衰减率 σt,我们可以假定整个材质中 σt 是均等的,例如在匀质胶体中。而对于一些大气中的云雾、烟雾,其内部各处的 σt 是不均等的,我们可以利用一个 3D Texture 储存和表示一个非均匀介质中各处的 σt,也可以基于解析函数实时计算,例如 3D Perlin Noise
Ray-marching

It’s really simple, but as often with raymarching it can quickly become expensive as it require a certain amount of rays to capture details, and that’s why the ray marching is done in a downscaled texture.
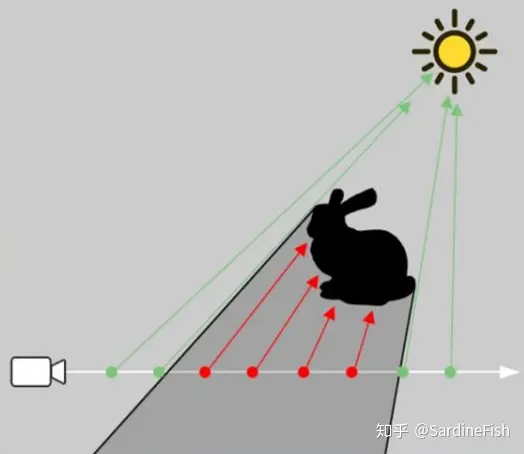
在实时渲染中,通常采用 ray-marching 的方式实现介质中散射光的渲染。即对屏幕上每个像素,计算从摄像机发出的视线光线,在介质中以一个特定的步长迭代步进,并在每次步进的位置向光源再做一次 ray-marching 计算入射光强度,再根据 phase function 和 transmittance function 计算从当前位置到摄像机的散射光强度。ray marching可以详见下文
参考《在 Unity 中实现体积光渲染》,其中提到,实时Ray-marching的代价巨大,因此可以对模型简化:
- 省略从光源入射到介质的透光率Transmittance积分。
- 估计入射光经过的距离和介质的平均衰减率(考虑均匀介质)。
- 根据效果需要,决定是否考虑阴影。
Simple Implementation
我们可以将体积渲染通过以下伪代码表示
float3 scattering(float3 ray, float near, float far)
{
float3 transmittance = 1;
float3 totalLight = 0;
for(float distance = near; distance < far; distance += StepSize)
{
float3 pos = CameraPosition + distance * ray;
float3 extinction = ExtinctionAt(pos);
transmittance *= exp(-StepSize * extinction);
float3 inScatterFactor = extinction - Absorbtion;
totalLight += transmittance * lightAt(pos) * inScatterFactor * Phase(lightDir, viewDir) * StepSize;
}
}
float3 lightAt(float3 pos)
{
float3 lightDir = DirectionTowardLight;
float3 transmittance = 1;
for(float len = 0; len < DistanceToLight; len += StepSize)
{
float x = pos + lightDir * len;
transmittance *= exp(-StepSize * ExtinctionAt(x));
}
float shadow = ShadowAt(pos);
return LightColor * transmittance * shadow;
}其中的 ExtinctionAt(x) 表示介质中 x 处的衰减率,可以表示为一个恒定的量(均匀介质),或是采样 3D Texture,或是用解析式计算。Phase(l,v) 可以根据需要,选择不同的 Phase Function 模型。ShadowAt(x) 可以通过采样 shadow map 实现。
式中采用累乘的方式步进计算 transmittance,避免多次积分计算,原理如下:
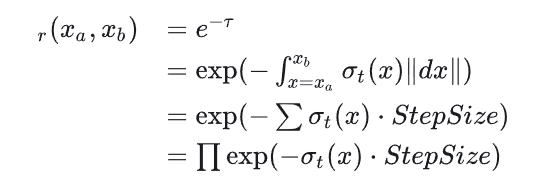
//TODO:非全局光源的设计和实现、unity URP的体积光实践,Moer内嵌体积光实践

