背包问题全解
1简单背包
我们通常使用一个二维数组表示这个背包的内容状态,比如f[num][weight]对应一定数量与重量的背包内容,然后遍历,从背包满载开始倒推。这里我们先采用二维DP的方式,虽然但是有的时候会引起MLE
设 DP 状态 dp[i][j]为在只能放前i个物品的情况下,容量为j的背包所能达到的最大总价值。
考虑转移。假设当前已经处理好了前 i-1个物品的所有状态,那么对于第i个物品,当其不放入背包时,背包的剩余容量不变,背包中物品的总价值也不变,故这种情况的最大价值为 f[i-1][j];当其放入背包时,背包的剩余容量会减小w[i] ,背包中物品的总价值会增大c[i],故这种情况的最大价值为 f[i-1][j-w[i]]+c[i]。
#include<cstdio>
using namespace std;
const int maxm=201,maxn=31;
int m,n;
int w[maxn],c[maxn];//weight and cost
int f[maxn][maxm];//f[数量][质量]
int max(int x,int y){
if(x<y)return y;
else return x;
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&w[i],&c[i]);
for(int i=1;i<=n;i++)
for(int v=m;v>0;v--)
if(w[i]<=v/*可以放包里*/)f[i][v]=max(f[i-1][v],f[i-1][v-w[i]]+c[i]);//不断推导当前数目放东西收益最大
else f[i][v]=f[i-1][v];
printf("%d",f[n][m]);
return 0;/*10 4
2 1
3 3
4 5
7 9*/
}二维背包比较碍事,而且fi只跟fi-1有关,所以可以去除一维
#include<cstdio>
using namespace std;
const int maxm=2001,maxn=31;
int m,n;
int w[maxn],c[maxn];//weight & cost
int f[maxm];
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&w[i],&c[i]);
for(int i=1;i<=n;i++)
for(int v=m;v>=w[i];v--)//只要放得下即可,并且不断压缩至正好
if(f[v-w[i]]+c[i]>f[v])f[v]=f[v-w[i]]+c[i];
printf("%d",f[m]);
return 0;
/*10 4
2 1
3 3
4 5
7 9*/
}在v的循环反向是为了不多放物体,因为0-1背包只能放一个
2完全背包
而与之相对应的完全背包则更加丰富,可以填充无数的同一个物体,代码实现如下:
#include<cstdio>
using namespace std;
const int maxm=201,maxn=31;
int m,n;
int w[maxn],c[maxn];
int f[maxm];
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&w[i],&c[i]);
for(int i=1;i<=n;i++)
for(int v=w[i];v<=m;v++)//可以逐渐填入一个w[i],两个w[i]······
if(f[v-w[i]]+c[i]>f[v])f[v]=f[v-w[i]]+c[i];
printf("%d\n",f[m]);
return 0;/*10 4
2 1
3 3
4 5
7 9*/
}
#include<cstdio>
using namespace std;
const int maxm=201,maxn=31;
int m,n;
int w[maxn],c[maxn];
int f[maxm];
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&w[i],&c[i]);
for(int i=1;i<=n;i++)
for(int v=w[i];v<=m;v++)//可以逐渐填入一个w[i],两个w[i]······
if(f[v-w[i]]+c[i]>f[v])f[v]=f[v-w[i]]+c[i];
printf("%d\n",f[m]);
return 0;/*10 4
2 1
3 3
4 5
7 9*/
}3多重背包
多重背包的特别之处,在于对每个物品施加了个数的限制,相比于0-1背包又可以多选物品,所以相比之下状态转移方程更加丰富。
#include<cstdio>
using namespace std;
int v[6002],w[6002],c[6002];
int f[6002];
int n,m;
int max(int x,int y){
if(x<y)return y;
else return x;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d%d",&v[i],&w[i],&c[i]);
for(int i=1;i<=n;i++)
for(int j=m;j>=0;j--)
for(int k=0;k<=c[i];k++)
{ if(j-k*v[i]<0)break;
f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
}
printf("%d",f[m]);
return 0;
}
/*5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1*/不如完全背包,这样的多重背包只能采取枚举,复杂度无法再优化

4一些优化:
+ 二进制优化

所以我们可以通过二进制分组的方式使得拆分方式更优美省时
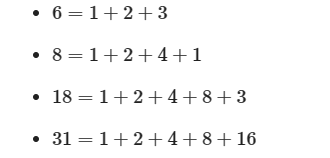
所以问题由此转换成0-1背包,解决即可。
index = 0;
for (int i = 1; i <= m; i++) {
int c = 1, p, h, k;
cin >> p >> h >> k;
while (k > c) {
k -= c;
list[++index].w = c * p;
list[index].v = c * h;
c *= 2;
}
list[++index].w = p * k;
list[index].v = h * k;
}其他优化好复杂先不写了
5.混合背包
混合背包就是将前面三种的背包问题混合起来,有的只能取一次,有的能取无限次,有的只能取k次。
这种题目看起来很吓人,可是只要领悟了前面几种背包的中心思想,并将其合并在一起就可以了。下面给出伪代码:
for (循环物品种类) {
if (是 0 - 1 背包)
套用 0 - 1 背包代码;
else if (是完全背包)
套用完全背包代码;
else if (是多重背包)
套用多重背包代码;
}6.二维背包
仍然是0-1背包问题,不过要增加一维存储新的价值
洛谷大佬题单
特点:码量较少(目前只有一题超过1KB)且难度较低,让新手也可以享受切题的快乐。
没学过背包问题的可以去看看洛谷日报中的背包问题或者背包九讲。
题目:
| 题目 | 题目解法 | 题目难度 | 实际难度 |
|---|---|---|---|
| P1048 采药 | 01背包 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P2871 [USACO07DEC]Charm Bracelet S | 01背包 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P1049 装箱问题 | 01背包稍微变形 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P1060 开心的金明 | 01背包稍微变形 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P1164 小A点菜 | 01背包稍微变形 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P1510 精卫填海 | 01背包稍微变形 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P2639 [USACO09OCT]Bessie’s Weight Problem G | 01背包稍微变形 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P2925 [USACO08DEC]Hay For Sale S | 01背包稍微变形 | $\color{#FF8C00}{\tt 普及-}$ | $\color{#FF8C00}{\tt 普及-}$ |
| P1926 小书童——刷题大军 | 01背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1802 5倍经验日 | 01背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1734 最大约数和 | 01背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P2392 kkksc03考前临时抱佛脚 | 01背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1466 [USACO2.2]集合 Subset Sums | 01背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FF8C00}{普及-}$ |
| P2370 yyy2015c01 的 U 盘 | 01背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FFD700}{普及/提高-}$ |
| CF294B Shaass and Bookshelf | 01背包变形 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| CF19B Checkout Assistant | 01背包变形 | $\color{#0000FF}{提高+/省选-}$ | $\color{#FFD700}{普及/提高-}$ |
| P4141 消失之物 | 01背包变形 | $\color{#0000FF}{提高+/省选-}$ | $\color{#32CD32}{普及+/提高}$ |
| P1156 垃圾陷阱 | 01背包变形 | $\color{#0000FF}{提高+/省选-}$ | $\color{#32CD32}{普及+/提高}$ |
| P1507 NASA的食物计划 | 二维01背包 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1910 L国的战斗之间谍 | 二维01背包 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1855 榨取kkksc03 | 二维01背包稍微变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1877 [HAOI2012]音量调节 | 二维01背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1509 找啊找啊找GF | 二维01背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FFD700}{普及/提高-}$ |
| P3985 不开心的金明 | 二维01背包变形 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| P1455 搭配购买 | 01背包+并查集 | $\color{#FFD700}{普及/提高-}$ | $\color{#FFD700}{普及/提高-}$ |
| P1941 飞扬的小鸟 | 01背包变形+完全背包变形 | $\color{#32CD32}{普及+/提高}$ | $\color{#32CD32}{普及+/提高}$ |
| P2170 选学霸 | 01背包变形+并查集 | $\color{#32CD32}{普及+/提高}$ | $\color{#32CD32}{普及+/提高}$ |
| P1858 多人背包 | 01背包 $k$ 优解变形 | $\color{#0000FF}{提高+/省选-}$ | $\color{#32CD32}{普及+/提高}$ |
| P1616 疯狂的采药 | 完全背包 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P2722 [USACO3.1]总分 Score Inflation | 完全背包 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1679 神奇的四次方数 | 完全背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1832 A+B Problem(再升级) | 完全背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P1853 投资的最大效益 | 完全背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FF8C00}{普及-}$ |
| CF189A Cut Ribbon | 完全背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FF8C00}{普及-}$ |
| CF417A Elimination | 完全背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FF8C00}{普及-}$ |
| P2918 [USACO08NOV]Buying Hay S | 完全背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FFD700}{普及/提高-}$ |
| P5662 纪念品 | 完全背包变形 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| P5020 [NOIP2018 提高组] 货币系统 | 完全背包变形 | $\color{#32CD32}{普及+/提高}$ | $\color{#32CD32}{普及+/提高}$ |
| P2347 砝码称重 | 多重背包变形 | $\color{#FF8C00}{普及-}$ | $\color{#FF8C00}{普及-}$ |
| P6771 [USACO05MAR]Space Elevator 太空电梯 | 多重背包变形 | $\color{#FFD700}{普及/提高-}$ | $\color{#FFD700}{普及/提高-}$ |
| P5365 [SNOI2017]英雄联盟 | 多重背包变形 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| P1776 宝物筛选 | 多重背包二进制优化 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| P2851 [USACO06DEC]The Fewest Coins G | 多重背包+完全背包 | $\color{#0000FF}{提高+/省选-}$ | $\color{#FFD700}{普及/提高-}$ |
| P1833 樱花 | 混合背包 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| P1782 旅行商的背包 | 混合背包二进制优化+完全背包+卡常 | $\color{#0000FF}{提高+/省选-}$ | $\color{#32CD32}{普及+/提高}$ |
| P1757 通天之分组背包 | 分组背包 | $\color{#FF8C00}{普及-}$ | $\color{#FFD700}{普及/提高-}$ |
| P5322 [BJOI2019]排兵布阵 | 分组背包变形 | $\color{#0000FF}{提高+/省选-}$ | $\color{#FFD700}{普及/提高-}$ |
| P1064 金明的预算方案 | 有依赖的背包 | $\color{#32CD32}{普及+/提高}$ | $\color{#FFD700}{普及/提高-}$ |
| P2904 [USACO08MAR]River Crossing S | 背包思想 | $\color{#FFD700}{普及/提高-}$ | $\color{#FFD700}{普及/提高-}$ |
最后:
1.如题目难度不符合实际,补充的题目或修改建议欢迎私信。
2.这个题单的题应该算比较简单,以后再写一个难一点的。
3.写题单不易,能不能帮忙收藏一下啊。
another 借鉴
27000字初级背包问题详解 – walker shi的文章 – 知乎

